题目内容
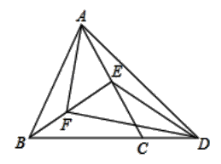
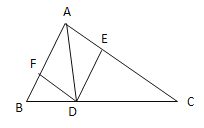
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中点,点
边上的中点,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() 沿
沿![]() 方向作匀速运动,点
方向作匀速运动,点![]() 从从顶点
从从顶点![]() 沿
沿![]() 方向同时出发,且它们的运动速度相同,连接
方向同时出发,且它们的运动速度相同,连接![]() ,
,![]() .
.
(1)求证:![]() .
.
(2)判断线段![]() 与
与![]() 的位置及数量关系,并说明理由.
的位置及数量关系,并说明理由.
(3)在运动过程中,![]() 与
与![]() 的面积之和是否为定值?若是,请求出这个定值;若不是,请说明理由.
的面积之和是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)证明见解析;(2)DE⊥DF,DE=DF,证明见解析;(3)△BDE与△CDF的面积之和始终是一个定值,这个定值为8.
【解析】
(1)由题意根据全等三角形的判定运用SAS,求证![]() 即可;
即可;
(2)根据全等三角形的性质结合中点和垂线定义,进行等量替换即可得出线段![]() 与
与![]() 的位置及数量关系;
的位置及数量关系;
(3)由题意根据全等三角形的性质得出S△BDE+S△CDF=S△ADF+S△CDF=S△ADC, 进而分析即可得知![]() 与
与![]() 的面积之和.
的面积之和.
解:(1)∵AB=AC,D是BC边上的中点,
∴AD是BC边上的高
又∵∠BAC=90°,
∴∠ABD=∠DAF=∠BAD=45°,
∴BD=AD
又由题意可知BE=AF,
∴△BDE≌△ADF(SAS).
(2)∵DE⊥DF,DE=DF,
理由如下:
∵△BDE≌△ADF,
∴DE=DF,∠BDE=∠ADF
∵AB=AC,D是BC边上的中点,
∴AD⊥BC,∠BDE+∠ADE=90°,
∴∠ADE+∠ADF=90°,DE⊥DF.
(3)在运动过程中,△BDE与△CDF的面积之和始终是一个定值
∵AB=AC,D是BC边上的中点,∠BAC=90°,
∴AD=BD=BC=4
又∵△BDE≌△ADF
S△BDE+S△CDF=S△ADF+S△CDF=S△ADC
又∵S△ADC=S△ABC=![]() .BC.AD=8
.BC.AD=8
∵点E,F在运动过程中,△ADC的面积不变,
∴△BDE与△CDF的面积之和始终是一个定值,这个定值为8.

 阅读快车系列答案
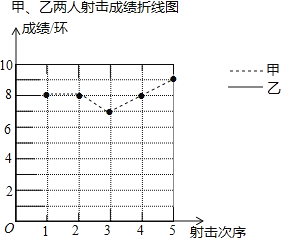
阅读快车系列答案【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为(单位:环):
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息,请解答下面的问题:
(1)α= ,b= ,c= ;
(2)完成图中表示乙成绩变化情况的折线;
(3)教练根据这5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(4)若选手乙再射击第6次,命中的成绩是8环,则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 .(填“变大”、“变小”或“不变”)