题目内容
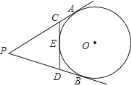
【题目】如图,![]() ,
,![]() 切
切![]() 于
于![]() 、
、![]() 两点,
两点,![]() 切
切![]() 于
于![]() 点,
点,![]() 的半径是
的半径是![]() ,
,![]() 周长为
周长为![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】
连接BO并延长交PA的延长线于F,连接OA,根据切线长定理得到PA=PB=2r,根据相似三角形的性质得到FB=2FA,根据勾股定理求出FB=![]() r,根据正切的概念计算得到答案.
r,根据正切的概念计算得到答案.
解:连接BO并延长交PA的延长线于F,连接OA,
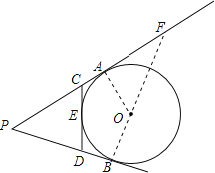
∵PA,PB切⊙O于A、B两点,CD切⊙O于E点,
∴PA=PB,CE=CA,DE=DB,
∴PA+PB=PC+PD+CD=4r,
∴PA=PB=2r,
∵PA,PB切⊙O于A、B,
∴∠FAO=∠FBP=90°,又∠AFO=∠BFP,
∴△FAO∽△FBP,
∴![]() =
=![]() ,
,
∴FB=2FA,
∴FA2+r2=(2FA-r)2,
解得,FA=![]() r,则FB=
r,则FB=![]() r,
r,
∴tan∠APB=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目