题目内容
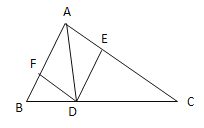
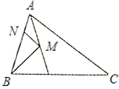
【题目】如图，在
中，
，
，
平分
，
、
分别是、
上的动点，当
最小时，
的度数为( )
A.
B.
C.
D.
【答案】B
【解析】
在AC上截取AE=AN，先证明△AME≌△AMN（SAS），推出ME=MN．当B、M、E共线，BE⊥AC时，BM+ME最小，可求出∠NME的度数，从而求出∠BMN的度数．
如图，在AC上截取AE=AN，
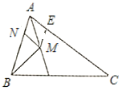
∵∠BAC的平分线交BC于点D，
∴∠EAM=∠NAM，
在△AME与△AMN中，
，
∴△AME≌△AMN（SAS），
∴ME=MN．
∴BM+MN=BM+ME，
当B、M、E共线，BE⊥AC时，BM+ME最小，
∴MN⊥AB
∵∠BAC=68°
∴∠NME=360°-∠BAC-∠MEA-∠MNA=360°-68°-90°-90°=112°，
∴∠BMN=180°-112°=68°．
故选：B．
练习册系列答案
相关题目
