题目内容
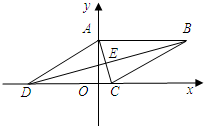 如图,四边形ABCD为菱形,已知A(0,6),D(-8,0).
如图,四边形ABCD为菱形,已知A(0,6),D(-8,0).(1)求点C的坐标;
(2)设菱形ABCD对角线AC、BD相交于点E,求经过点E的反比例函数解析式.
分析:(1)根据菱形的性质和给出的数据,利用勾股定理即可求出C点的坐标;
(2)经过点E的反比例函数解析式为y=
(k≠0),再求出E点的坐标,代入求出K即可.
(2)经过点E的反比例函数解析式为y=
| k |
| x |
解答:解:(1)∵A(0,6),D(-8,0),
∴OA=6,OD=8,
∴由勾股定理可得AD=10,
∵四边形ABCD为菱形∴CD=AD=10,
∴OC=2,
∴C(2,0),
(2)∵A(0,6)C(2,0),
∴E(1,3),
设经过点E的反比例函数解析式为y=
(k≠0),将E(1,3)代入求得k=3
∴反比例函数解析式为:y=
.
∴OA=6,OD=8,
∴由勾股定理可得AD=10,
∵四边形ABCD为菱形∴CD=AD=10,
∴OC=2,
∴C(2,0),
(2)∵A(0,6)C(2,0),
∴E(1,3),
设经过点E的反比例函数解析式为y=
| k |
| x |
∴反比例函数解析式为:y=
| 3 |
| x |
点评:本题考查了菱形的性质和勾股定理的运用以及点的坐标和点到坐标轴的距离与这个点的坐标的区别,主要表现在两个方面:①到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.