题目内容
如图,在正方形 中,
中, ,点
,点 是边
是边 上的任意一点,
上的任意一点, 是
是 延长线上一点,联结
延长线上一点,联结 ,作
,作 交
交 的平分线
的平分线 上一点
上一点 ,联结
,联结 交边
交边 于点
于点 .
.

(1)求证: ;
;
(2)设点 到点
到点 的距离为
的距离为 ,线段
,线段 的长为
的长为 ,试求
,试求 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)当点 是线段
是线段 延长线上一动点,那么(2)式中
延长线上一动点,那么(2)式中 与
与 的函数关系式保持不变吗?如改变,试直接写出函数关系式.
的函数关系式保持不变吗?如改变,试直接写出函数关系式.
 中,
中, ,点
,点 是边
是边 上的任意一点,
上的任意一点, 是
是 延长线上一点,联结
延长线上一点,联结 ,作
,作 交
交 的平分线
的平分线 上一点
上一点 ,联结
,联结 交边
交边 于点
于点 .
.
(1)求证:
 ;
;(2)设点
 到点
到点 的距离为
的距离为 ,线段
,线段 的长为
的长为 ,试求
,试求 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)当点
 是线段
是线段 延长线上一动点,那么(2)式中
延长线上一动点,那么(2)式中 与
与 的函数关系式保持不变吗?如改变,试直接写出函数关系式.
的函数关系式保持不变吗?如改变,试直接写出函数关系式.(1)证明见解析;(2)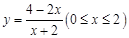 ;(3)改变,
;(3)改变, .
.
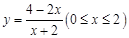 ;(3)改变,
;(3)改变, .
.试题分析:(1)欲证
 利用原图无法证明,需构建三角形且使之全等,因此在边
利用原图无法证明,需构建三角形且使之全等,因此在边 上截取线段
上截取线段 ,使
,使 ,连接
,连接 ,证明
,证明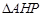 与
与 全等即可.
全等即可.(2)由
 ∽
∽ 列式化简即可得.
列式化简即可得.(3)在
 延长线上取点
延长线上取点 ,令
,令 ,
,∴
 是等腰直角三角形.∴
是等腰直角三角形.∴ .
.同理,
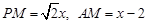 ,
,∵
 ,
,∴
 ∽
∽ .
.∴
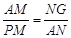 ,即
,即 .
.整理,得
 .
.
试题解析:(1)在边
 上截取线段
上截取线段 ,使
,使 ,连接
,连接 ,
,由正方形
 ,得
,得 ,
,∵
 ,∴
,∴ .
.∵
 ,∴
,∴ .
.又∵
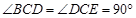 ,
, 平分
平分 ,∴
,∴ .∴
.∴ .
.又∵
 ,∴
,∴ ,即得
,即得 .
.∴
 ,即得
,即得 .
.在
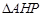 和
和 中,
中,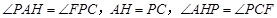 ,
,∴
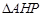 ≌
≌ ,
,∴
 .
.
(2)在
 上取点
上取点 ,令
,令 ,
,∴
 是等腰直角三角形.∴
是等腰直角三角形.∴ .
.同理,
 ,
,∵
 ,
,∴
 ∽
∽ .
.∴
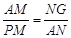 ,即
,即 .
.整理,得
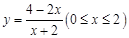 .
.(3)改变,
 .
.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目


 =4,则梯形ABCD的面积为_________.
=4,则梯形ABCD的面积为_________.




 中,
中, ,
,
 平分
平分 交
交 边于点
边于点 ,且
,且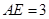 ,则
,则 的长为( )
的长为( )
