Question

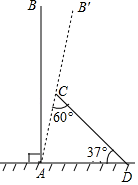
【题目】某次台风来袭时，一棵笔直大树树干AB（假定树干AB垂直于水平地面）被刮倾斜7°（即∠BAB′＝7°）后折断倒在地上，树的顶部恰好接触到地面D处，测得∠CDA＝37°，AD＝5米，求这棵大树AB的高度．（结果保留根号）（参考数据：sin37≈0.6，cos37＝0.8，tan37≈0.75）

Answer 1

【答案】（3+4）米．

【解析】

过点A作AE⊥CD于点E，解Rt△AED，求出DE及AE的长度，再解Rt△AEC，得出CE及AC的长，进而可得出结论．

解：过点A作AE⊥CD于点E，则∠AEC＝∠AED＝90．

∵在Rt△AED中，∠ADC＝37，

∴cos37＝，

∴DE＝4，

∵sin37＝，

∴AE＝3，

在Rt△AEC中，

∵∠CAE＝90﹣∠ACE＝90﹣60＝30，

∴CE＝AE＝，

∴AC＝2CE＝2，

∴AB＝AC+CE+ED＝2++4＝3+4（米）．

答：这棵大树AB原来的高度是（3+4）米．