题目内容
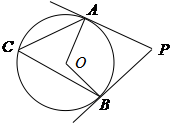
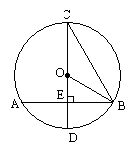
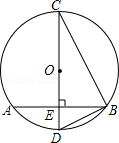
如图,在⊙O中,直径CD垂直于弦AB于点E,连接OB、CB,已知⊙O的半径为2,AB= ,则∠BCD= 度.
,则∠BCD= 度.
 ,则∠BCD= 度.
,则∠BCD= 度.
30°.
试题分析:由垂径定理知:BE=
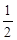 AB=
AB=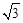 ,在Rt△OBE中,可求出∠BOE的度数,利用圆周角与圆心角的关系可求出∠BCD的度数.
,在Rt△OBE中,可求出∠BOE的度数,利用圆周角与圆心角的关系可求出∠BCD的度数.试题解析:∵CD⊥AB,且AB=

∴BE=
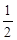 AB=
AB=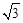
在Rt△OBE中,sin∠BOE=
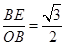 .
.∴∠BOE=60°
∴
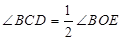 =30°.
=30°.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
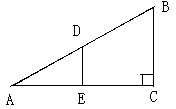
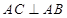 ,
,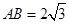 ,
,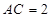 ,点
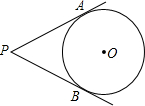
,点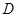 是以
是以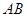 为直径的半圆
为直径的半圆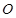 上一动点,
上一动点,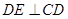 交直线
交直线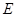 ,设
,设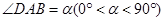 .
.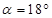 时,求弧BD的长;
时,求弧BD的长;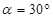 时,求线段
时,求线段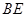 的长;
的长;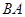 的延长线上,则
的延长线上,则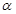 的取值范围是_________.(直接写出答案)
的取值范围是_________.(直接写出答案)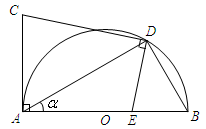
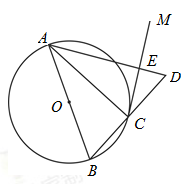

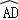 =
=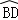 C.OE=DE D.∠DBC=90°
C.OE=DE D.∠DBC=90°