题目内容
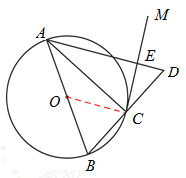
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC = CD,连接AD与CM交于点E,若⊙O的半径为3,ED = 2,求∆ACE的外接圆的半径.
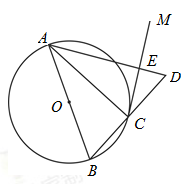
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC = CD,连接AD与CM交于点E,若⊙O的半径为3,ED = 2,求∆ACE的外接圆的半径.

(1)证明见解析;(2)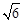 .
.
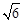 .
.试题分析:(1)连接OC,根据圆周角定理、切线的性质和等腰三角形等边对等角的性质,应用角的转换即可证得结论.
(2)由已知可得OC是△ABC的中位线,从而可得ΔAEC是直角三角形,即AEC的外接圆的直径为AC,通过证明ΔABC∽ΔCDE求得BC的长,在RtΔABC中应用勾股定理求出AC的长,从而得到∆ACE的外接圆的半径.
试题解析:(1)如图,连接OC,
∵AB为⊙O的直径,∴∠ACB =" 90°." ∴∠ABC+∠BAC= 90°.
又∵CM是⊙O的切线,∴OC⊥CM. ∴∠ACM+∠ACO=" 90°" .
∵CO = AO,∴∠BAC =∠ACO. ∴∠ACM =∠ABC.
(2)∵BC = CD,BO = OA,∴OC∥AD.
又∵OC⊥CE. ∴AD⊥CE. ∴ΔAEC是直角三角形. ∴ΔAEC的外接圆的直径为AC.
又∵∠ABC+∠BAC= 90°,∠ACM+∠ECD = 90°,∠ABC =∠ACM,∴∠BAC =∠ECD.
又∵∠CED =∠ACB = 90°,∴ΔABC∽ΔCDE. ∴
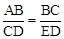 .
.∵⊙O的半径为3,ED = 2,∴AB = 6.∴
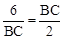 ,解得
,解得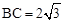 .
.∴在RtΔABC中,
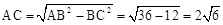 .
.∴ ΔAEC的外接圆的半径为
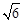 .
.
练习册系列答案
相关题目
 ,则∠BCD= 度.
,则∠BCD= 度.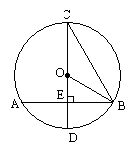
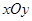 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点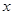 轴交于
轴交于 ,
,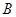 两点,
两点, 为弦,
为弦,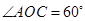 ,
,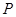 是
是 。
。 的度数为 ;
的度数为 ;  的长;
的长;  上时,
上时, ,问
,问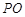 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?
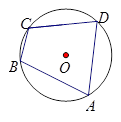
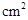

 CD,垂足为E,连接BC,若AB=
CD,垂足为E,连接BC,若AB=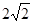 cm,
cm,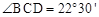 ,则圆O的半径为 cm.
,则圆O的半径为 cm.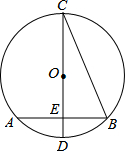
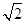 ,则∠BAC的度数是()
,则∠BAC的度数是()