题目内容
【题目】已知AB是⊙O的直径，弦CD与AB相交，∠BAC＝40°．
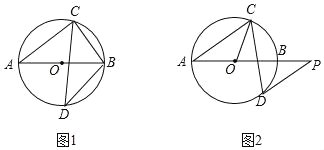
（1）如图1，若D为弧AB的中点，求∠ABC和∠ABD的度数；
（2）如图2，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的度数．
【答案】（1）45°；（2）26°．
【解析】
（1）根据圆周角和圆心角的关系和图形可以求得∠ABC和∠ABD的大小；
（2）根据题意和平行线的性质、切线的性质可以求得∠OCD的大小．
（1）∵AB是⊙O的直径，∠BAC=38°， ∴∠ACB=90°，
∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°，
∵D为弧AB的中点，∠AOB=180°，∴∠AOD=90°，
∴∠ABD=45°；
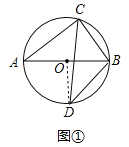
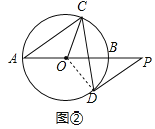
（2）连接OD，
∵DP切⊙O于点D，∴OD⊥DP，即∠ODP=90°，
∵DP∥AC，∠BAC=38°，∴∠P=∠BAC=38°，
∵∠AOD是△ODP的一个外角，
∴∠AOD=∠P+∠ODP=128°，∴∠ACD=64°，
∵OC=OA，∠BAC=38°，∴∠OCA=∠BAC=38°，
∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某公司生产一种原料，运往A地和B地销售．如表记录的是该产品运往A地和B地供应量y1（kg）、y2（kg）与销售价格x（元）之间的关系：
销售价格x（元） | 100 | 150 | 200 | 300 |
运往A地y1（kg） | 300 | 250 | 200 | 100 |
运往B地y2（kg） | 450 | 350 | 250 | n |
（1）请认真分析上表中所给数据，用你所学过的函数来表示其变化规律，并验证你的猜想，分别求出y1与x、y2与x的函数关系式；
（2）用你求出的函数关系式完成上表，直接写出n＝ ；
（3）直接写出销售价格在 元时，该产品运往A地的供应量等于运往B地的供应量．
