Question

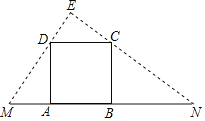
【题目】如图，在边长为6的正方形ABCD的一边AB在线段MN上移动，连接MD，NC并延长交于点E，MN＝18．

（1）当AM＝4时，求CN长；

（2）若∠E＝90°，求证AM＝BN；

（3）△MNE能否为等腰三角形？若能，求出AM的长，若不能，请说明理由．

Answer 1

【答案】（1）10；（2）见解析；（3）△MNE能为等腰三角形，AM＝6．

【解析】

（1）先求BN的长，由勾股定理可求CN的长；

（2）通过证明△ADM∽△BNC，可得，可求AM＝6＝BN；

（3）分三种情况讨论，由全等三角形的判定和性质和等腰三角形的性质可求解．

（1）∵四边形ABCD是正方形，

∴AB＝AD＝BC＝6，∠DAB＝∠ABC＝90°，

∵AM＝4，MN＝18，AB＝6，

∴BN＝8，

在Rt△BCN中，CN＝＝10；

（2）∵∠E＝90°，

∴∠M+∠N＝90°，且∠M+∠ADM＝90°，

∴∠N＝∠ADM，且∠DAM＝∠CBN＝90°，

∴△ADM∽△BNC，

∴，

∴

∴36＝AM×BN＝AM（12﹣AM）

∴AM＝6，

∴BN＝6，

∴AM＝BN；

（3）△MNE能为等腰三角形，

若EM＝EN，

∴∠M＝∠N，且AD＝BC，∠DAM＝∠CBN，

∴△ADM≌△BCN（AAS）

∴AM＝BN，

∵MN＝AB+AM+BN＝18，AB=6，

∴2AM＝12，

∴AM＝6；

若MN＝EN＝18，

∴∠M＝∠E，

∵CD∥MN，

∴∠EDC＝∠M＝∠E，

∴EC＝CD＝6，

∴CN＝12，

∴BN＝，

∴AM＝MN﹣AB﹣BN＝12﹣6，

若MN＝EM＝18，

∴∠N＝∠E，

∵CD∥MN，

∴∠ECD＝∠N＝∠E，

∴ED＝CD＝6，

∴DM＝12，

∴AM＝．