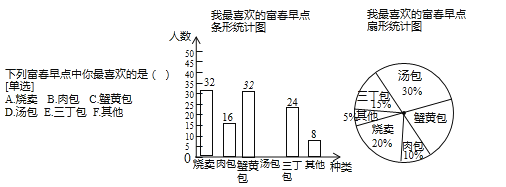
题目内容
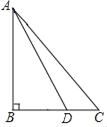
【题目】如图,直角三角形ABC中,∠ACB=900,AB=10, BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1.若△E1FA1∽△E1BF,则AD= .

【答案】3.2。
【解析】
∵∠ACB=900,AB=10,BC=6,∴![]() 。
。
设AD=2x,
∵点E为AD的中点,将△ADF沿DF折叠,点A对应点记为A1,点E的对应点为E1,
∴AE=DE=DE1=A1E1=x。
∵DF⊥AB,∠ACB=900,∠A=∠A,∴△ABC∽△AFD。
∴AD:AC =DF:BC ,即2x:8 =DF:6 ,解得DF=1.5x。
在Rt△DE1F中,E1F2= DF2+DE12=" 3.25" x2,
又∵BE1=AB-AE1=10-3x,△E1FA1∽△E1BF,∴E1F:A1E1=BE1:E1F ,即E1F2=A1E1BE1。
∴![]() ,解得x="1.6" 或x=0(舍去)。
,解得x="1.6" 或x=0(舍去)。
∴AD的长为2×1.6 =3.2。

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目