Question

如图在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，且点A（0，2），点C（-1，0），如图所示点B在抛物线y=ax²+ax-2上．
（1）求点B的坐标；
（2）求抛物线的解析式；
（3）将三角板ABC绕顶点A逆时针方向旋转90°到达△AB′C′的位置，请写出点B′坐标

（1，-1）

，点C′坐标

（2，1）

；判断点B′

在

，C′

在

（填“在”或“不”）在（2）中的抛物线上．

Answer 1

分析：（1）根据题意，过点B作BD⊥x轴，垂足为D；根据角的互余的关系，易得B到x、y轴的距离，即B的坐标；
（2）根据抛物线过B点的坐标，可得a的值，进而可得其解析式；
（3）本题的关键是求出B′，C′两点的坐标．过点B′作B′M⊥y轴于点M，过点B作BN⊥y轴于点N，过点C″作C″P⊥y轴于点P．然后仿照（1）中求坐标时的方法，通过证Rt△AB′M≌Rt△BAN来得出B′的坐标．同理可得出C′的坐标．然后将两点的坐标分别代入抛物线的解析式中，进而可判断出两点是否在抛物线上．

解答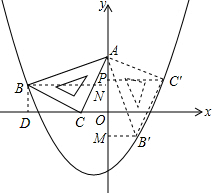：解：（1）过点B作BD⊥x轴，垂足为D，
∵∠BCD+∠ACO=90°，∠ACO+∠CAO=90°，
∴∠BCD=∠CAO，
又∵∠BDC=∠COA=90°，CB=AC，
∴△BCD≌△CAO，
∴BD=OC=1，CD=OA=2，
∴点B的坐标为（-3，1）；

（2）∵抛物线y=ax²+ax-2经过点B（-3，1），
∴1=9a-3a-2，解得a=

1

2

，
∴抛物线的解析式为：y=

1

2

x²+

1

2

x-2；

（3）如图，过点B′作B′M⊥y轴于点M，过点B作BN⊥y轴于点N，过点C″作C″P⊥y轴于点P，
在Rt△AB′M与Rt△BAN中，
∵∠AMB'=∠ANB=90°，∠AB′M=∠BAN=90°-∠B′AM，
∴∠ABN=∠B′AM，
在Rt△AB′M与Rt△BAN．
∵

∠AB′M=∠BAN AB=AB′ ∠ABN=∠B′AM

，
∴Rt△AB′M≌Rt△BAN．
∴B′M=AN=1，AM=BN=3，
∴B′（1，-1）．
同理△AC′P≌△CAO，C′P=OA=2，AP=OC=1，可得点C′（2，1）；
将点B′、C′的坐标代入y=x²+x-2，可知点B′、C′在抛物线上．
故答案为：（1，-1），（2，1），在，在．

点评：本题考查的是二次函数综合题，重点考查的是待定系数法求二次函数解析式、三角形全等、图形旋转变换等重要知识点；综合性强，考查学生数形结合的数学思想方法．