题目内容
 如图在平面直角坐标系中,M为x轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为
如图在平面直角坐标系中,M为x轴上一点,⊙M交x轴于A、B两点,交y轴于C、D两点,P为 |
| BC |
(1)求C点坐标;
(2)当点P在
 |
| BC |
(3)当点P在
 |
| BC |
分析:(1)连接MC,由A、M的坐标可得出OA、OM、以及MA的值,再在Rt△OCM中,OC=
,从而求出点C的坐标;
(2)作辅助线,连接AC,根据圆周角推论,等弧所对的圆周角相等,可得:∠ACD=∠P,又CQ平分∠OCP,可得:∠PCQ=∠OCQ,故:∠ACD+∠OCQ=∠PCQ+∠P,即∠ACQ=∠AQC,所以AQ=AC=2为定值;
(3)假设存在这样的点P满足条件,则点C、Q、M三点共线,所以CM平分平分∠PCD.由特殊角的三角形函数值求得∠OCM=30°,则易求∠DCP=60°.据此可以求得点P的坐标.
| 3 |
(2)作辅助线,连接AC,根据圆周角推论,等弧所对的圆周角相等,可得:∠ACD=∠P,又CQ平分∠OCP,可得:∠PCQ=∠OCQ,故:∠ACD+∠OCQ=∠PCQ+∠P,即∠ACQ=∠AQC,所以AQ=AC=2为定值;
(3)假设存在这样的点P满足条件,则点C、Q、M三点共线,所以CM平分平分∠PCD.由特殊角的三角形函数值求得∠OCM=30°,则易求∠DCP=60°.据此可以求得点P的坐标.
解答: 解:(1)如图1,连接MC.
解:(1)如图1,连接MC.
∵A(-1,0),M(1,0),
∴OA=OM=1,MA=CM=2.
在Rt△OCM中,OM=1,CM=2,
根据勾股定理得:OC=
=
,
∴点C的坐标是(0,
);
(2)如图1,连接AC.当P点运动时,线段AQ的长度不改变.理由如下:
由垂径定理知:
=
,
∴∠P=∠ACD,
∵CQ平分∠PCD,
∴∠P+∠PCQ=∠ACD+∠DCQ,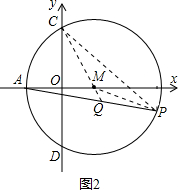
即:∠AQC=∠ACQ,
∴AQ=AC.
在Rt△OCA中,OC=
,OA=1,
∴AC=2.即线段AQ的长度为2.
(3)当点P在
上运动时,存在这样的点P,使CQ所在直线经过点M.理由如下:
假设当点P在
上运动时,存在这样的点P,使CQ所在直线经过点M.则点C、Q、M三点共线,
∵CQ平分∠PCD,
∴CM平分平分∠PCD.
在直角△OCM中,OM=1,OC=
,则tan∠OCM=
=
,
∴∠OCM=30°,
∴∠MCP=∠MPC=30°.
∴∠CMP=180°-2×30°=120°,
∴∠AMC=60°.
又∵∠APC=
∠AMC=30°,
∴∠APC=∠MPC,则点M、Q重合,即P与点B重合,
∴AP=4,
∴AQ=AM=2,这与线段AQ的长是2相一致,
∴当点P在
上运动时,存在这样的点P,使CQ所在直线经过点M,此时P(3,0).
 解:(1)如图1,连接MC.
解:(1)如图1,连接MC.∵A(-1,0),M(1,0),
∴OA=OM=1,MA=CM=2.
在Rt△OCM中,OM=1,CM=2,
根据勾股定理得:OC=
| CM2-OM2 |
| 3 |
∴点C的坐标是(0,
| 3 |
(2)如图1,连接AC.当P点运动时,线段AQ的长度不改变.理由如下:
由垂径定理知:
 |
| AC |
 |
| AD |
∴∠P=∠ACD,
∵CQ平分∠PCD,
∴∠P+∠PCQ=∠ACD+∠DCQ,

即:∠AQC=∠ACQ,
∴AQ=AC.
在Rt△OCA中,OC=
| 3 |
∴AC=2.即线段AQ的长度为2.
(3)当点P在
 |
| BC |
假设当点P在
 |
| BC |
∵CQ平分∠PCD,
∴CM平分平分∠PCD.
在直角△OCM中,OM=1,OC=
| 3 |
| OM |
| OC |
| ||
| 3 |
∴∠OCM=30°,
∴∠MCP=∠MPC=30°.
∴∠CMP=180°-2×30°=120°,
∴∠AMC=60°.
又∵∠APC=
| 1 |
| 2 |
∴∠APC=∠MPC,则点M、Q重合,即P与点B重合,
∴AP=4,
∴AQ=AM=2,这与线段AQ的长是2相一致,
∴当点P在
 |
| BC |
点评:本题考查圆的综合题.解此类问题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
相关题目
 21、如图在平面直角坐标系中,△AOB的顶点分别为A(2,0),O(0,0),B(0,4).
21、如图在平面直角坐标系中,△AOB的顶点分别为A(2,0),O(0,0),B(0,4). 如图在平面直角坐标系xOy中,点A的坐标为(2,0),以点A为圆心,2为半径的圆与x轴交于O,B两点,C为⊙A上一点,P是x轴上的一点,连接CP,将⊙A向上平移1个单位长度,⊙A与x轴交于M、N,与y轴相切于点G,且CP与⊙A相切于点C,∠CAP=60°.请你求出平移后MN和PO的长.
如图在平面直角坐标系xOy中,点A的坐标为(2,0),以点A为圆心,2为半径的圆与x轴交于O,B两点,C为⊙A上一点,P是x轴上的一点,连接CP,将⊙A向上平移1个单位长度,⊙A与x轴交于M、N,与y轴相切于点G,且CP与⊙A相切于点C,∠CAP=60°.请你求出平移后MN和PO的长. 如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示点B在抛物线y=ax2+ax-2上.
如图在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示点B在抛物线y=ax2+ax-2上. 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.