ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ£ђґюіќЇѓ э![]() µƒЌЉѕс”л
µƒЌЉѕс”л![]() ÷бљї”Џ
÷бљї”Џ![]() °Ґ
°Ґ![]() Ѕљµг£ђ”л
Ѕљµг£ђ”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђ
£ђ![]() £Ѓµг
£Ѓµг![]() ‘ЏЇѓ эЌЉѕс…ѕ£ђ
‘ЏЇѓ эЌЉѕс…ѕ£ђ![]() ÷б£ђ«“
÷б£ђ«“![]() £ђ÷±ѕя
£ђ÷±ѕя![]() «≈„ќпѕяµƒґ‘≥∆÷б£ђ
«≈„ќпѕяµƒґ‘≥∆÷б£ђ![]() «≈„ќпѕяµƒґ•µг£Ѓ
«≈„ќпѕяµƒґ•µг£Ѓ
£®1£©«у![]() °Ґ
°Ґ![]() µƒ÷µ£ї
µƒ÷µ£ї
£®2£©»зЌЉҐў£ђЅђљ”![]() £ђѕяґќ
£ђѕяґќ![]() …ѕµƒµг
…ѕµƒµг![]() єЎ”Џ÷±ѕя
єЎ”Џ÷±ѕя![]() µƒґ‘≥∆µг
µƒґ‘≥∆µг![]() «°Ї√‘Џѕяґќ
«°Ї√‘Џѕяґќ![]() …ѕ£ђ«уµг
…ѕ£ђ«уµг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
£®3£©»зЌЉҐЏ£ђґѓµг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ£ђєэµг
…ѕ£ђєэµг![]() „ч
„ч![]() ÷бµƒієѕяЈ÷±р”л
÷бµƒієѕяЈ÷±р”л![]() љї”Џµг
љї”Џµг![]() £ђ”л≈„ќпѕяљї”Џµг
£ђ”л≈„ќпѕяљї”Џµг![]() £Ѓ ‘ќ £Ї≈„ќпѕя…ѕ «Јсіж‘Џµг
£Ѓ ‘ќ £Ї≈„ќпѕя…ѕ «Јсіж‘Џµг![]() £ђ єµ√
£ђ єµ√![]() ”л
”л![]() µƒ√жїэѕаµ»£ђ«“ѕяґќ
µƒ√жїэѕаµ»£ђ«“ѕяґќ![]() µƒ≥§ґ»„о–°£њ»зєыіж‘Џ£ђ«у≥цµг
µƒ≥§ґ»„о–°£њ»зєыіж‘Џ£ђ«у≥цµг![]() µƒ„ш±к£ї»зєы≤їіж‘Џ£ђЋµ√чјн”…£Ѓ
µƒ„ш±к£ї»зєы≤їіж‘Џ£ђЋµ√чјн”…£Ѓ
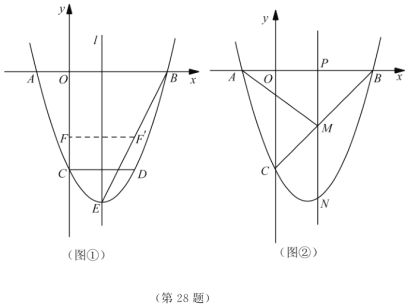
°Њір∞Є°њ£®1£©![]() £ђ
£ђ![]() £ї£®2£©µг
£ї£®2£©µг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]() £ї£®3£©µг
£ї£®3£©µг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]() ЇЌ
ЇЌ![]()
°Њљвќц°њ
‘ћвЈ÷ќц£Ї £®1£©ЄщЊЁґюіќЇѓ эµƒґ‘≥∆÷бєЂ љ£ђ≈„ќпѕя…ѕµƒµгіъ»л£ђЉіњ…£ї£®2£©ѕ»«уFµƒґ‘≥∆µг£ђіъ»л÷±ѕяBE£ђЉіњ…£ї£®3£©єє‘м–¬µƒґюіќЇѓ э£ђјы”√∆д–‘÷ «уЉЂ÷µ.
‘ћвљвќц£Ї.љв£Ї£®1£©![]() ÷б£ђ
÷б£ђ![]() £ђ
£ђ![]() ≈„ќпѕяґ‘≥∆÷бќ™÷±ѕя
≈„ќпѕяґ‘≥∆÷бќ™÷±ѕя![]()
![]()
![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]()
![]() љвµ√
љвµ√![]() їт
їт![]() £®…б»•£©£ђ
£®…б»•£©£ђ![]()
£®2£©…иµг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]()
![]() ґ‘≥∆÷бќ™÷±ѕя
ґ‘≥∆÷бќ™÷±ѕя![]() µг
µг![]() єЎ”Џ÷±ѕя
єЎ”Џ÷±ѕя![]() µƒґ‘≥∆µг
µƒґ‘≥∆µг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]() .
.
![]() ÷±ѕя
÷±ѕя![]() Њ≠єэµг
Њ≠єэµг![]() јы”√іэґ®ѕµ эЈ®њ…µ√÷±ѕя
јы”√іэґ®ѕµ эЈ®њ…µ√÷±ѕя![]() µƒ±ніп љќ™
µƒ±ніп љќ™![]() .
.
“тќ™µг![]() ‘Џ
‘Џ![]() …ѕ£ђ
…ѕ£ђ![]()
![]() Љіµг
Љіµг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]()
£®3£©іж‘Џµг![]() ¬ъ„гћв“в.…иµг
¬ъ„гћв“в.…иµг![]() „ш±кќ™
„ш±кќ™![]() £ђ‘т
£ђ‘т![]()
„ч![]() іє„гќ™
іє„гќ™![]()
![]()
![]()
Ґўµг![]() ‘Џ÷±ѕя
‘Џ÷±ѕя![]() µƒ„у≤а ±£ђ
µƒ„у≤а ±£ђ![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]()
![]() ‘Џ
‘Џ![]() ÷–£ђ
÷–£ђ![]() ±£ђ
±£ђ![]() »°„о–°÷µ
»°„о–°÷µ![]() .іЋ ±
.іЋ ±![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]()
ҐЏµг![]() ‘Џ÷±ѕя
‘Џ÷±ѕя![]() µƒ”“≤а ±£ђ
µƒ”“≤а ±£ђ![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]() Ќђјн£ђ
Ќђјн£ђ![]() ±£ђ
±£ђ![]() »°„о–°÷µ
»°„о–°÷µ![]() .іЋ ±
.іЋ ±![]() µгµƒ„ш±кќ™
µгµƒ„ш±кќ™![]()
„џ…ѕЋщ ц£Ї¬ъ„гћв“вµ√µг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]() ЇЌ
ЇЌ![]()




