题目内容
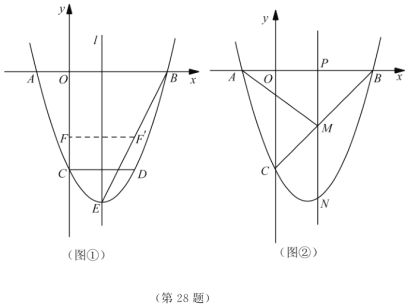
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),将该抛物线位于
的左侧),将该抛物线位于![]() 轴上方曲线记作
轴上方曲线记作![]() ,将该抛物线位于
,将该抛物线位于![]() 轴下方部分沿
轴下方部分沿![]() 轴翻折,翻折后所得曲线记作
轴翻折,翻折后所得曲线记作![]() ,曲线
,曲线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求曲线![]() 所在抛物线相应的函数表达式;
所在抛物线相应的函数表达式;
(2)求![]() 外接圆的半径;
外接圆的半径;
(3)点![]() 为曲线
为曲线![]() 或曲线
或曲线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,若以点
轴上的一个动点,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)
;(2) ![]() ;(3)点
;(3)点![]() 的坐标分别为
的坐标分别为![]()
![]() .
.
【解析】
试题分析:(1) 把![]() 化为顶点式,求得该抛物线的顶点坐标和开口方向,由翻折可得曲线
化为顶点式,求得该抛物线的顶点坐标和开口方向,由翻折可得曲线![]() 所在抛物线的顶点坐标和开口方向,即可得曲线
所在抛物线的顶点坐标和开口方向,即可得曲线![]() 的解析式;(2)先求得
的解析式;(2)先求得![]() 外接圆圆心的坐标,再利用勾股定理求得半径的长即可;(3)分点P位于曲线M上和点P位于曲线N上两种情况求点Q的坐标即可.
外接圆圆心的坐标,再利用勾股定理求得半径的长即可;(3)分点P位于曲线M上和点P位于曲线N上两种情况求点Q的坐标即可.
试题解析:(1)因为![]() 可化为
可化为![]() ,
,
所以抛物线![]() 的点的坐标为(1,-4),开口向上,
的点的坐标为(1,-4),开口向上,
所以曲线![]() 所在抛物线的顶点坐标为(1,4),开口向下,
所在抛物线的顶点坐标为(1,4),开口向下,
故曲线![]() 所在抛物线相应的函数表达式为
所在抛物线相应的函数表达式为![]() ,
,
即![]() ;
;
(2)因为抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,
所以A(-1,0),B(3,0),则线段AB的垂直平分线的直线为x=1,
因为曲线![]() 交
交![]() 轴于点(0,3),
轴于点(0,3),
所以OC=OB,又∠COB=90°,所以线段BC的垂直平分线为直线y=x,
联立![]() ,解得
,解得![]() ,所以△ABC的外接圆圆心坐标为(1,1),
,所以△ABC的外接圆圆心坐标为(1,1),
由勾股定理可得![]() ,所以△ABC的外接圆半径为
,所以△ABC的外接圆半径为![]() ;
;
(3)过点C作直线l∥x轴,交曲线M或N于点P,
①当点P位于曲线M上时,
由![]() ,解得
,解得![]() ,
,
所以CP=![]() ,H或CP=
,H或CP=![]() ;
;
因为以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
所以CP∥BQ且CP=BQ,
所以![]() ;
;
②当点P位于曲线N上时,
由![]() ,解得
,解得![]() (舍去),
(舍去),
所以CP=2;
因为以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
所以CP∥BQ且CP=BQ,
所以![]() ;
;
综上所述,点![]() 的坐标分别为
的坐标分别为![]()
![]() .
.


【题目】某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
时间 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
新加入人数(人) | 153 | 550 | 653 | b | 725 |
累计总人数(人) | 3353 | 3903 | a | 5156 | 5881 |
(1)表格中a= ,b= ;
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是 (只要填写正确说法前的序号).
①在活动之前,该网站已有3200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2528人.