题目内容
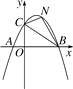
【题目】如图,抛物线y=-![]() [(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
(1)求m,n的值;
(2)点N为抛物线上的一动点,且位于直线BC上方,连接CN,BN.求△NBC面积的最大值.
【答案】(1)m=1,n=-9;(2)![]() .
.
【解析】试题分析:(1)由抛物线解析式可得出抛物线的对称轴为直线x=2,又由点A和点B是抛物线与x轴的交点,则A和B关于对称轴对称,则![]() =2,便可求得m,得出点A和点B坐标,将A坐标代入抛物线便求得n;
=2,便可求得m,得出点A和点B坐标,将A坐标代入抛物线便求得n;
(2)过点N作ND∥y轴交BC于D.先求得BC解析式,设点N坐标(x,-![]() x2+
x2+![]() x+3),便可得点D坐标,则得ND的值,由S△NBC=S△NDC+S△NDB=
x+3),便可得点D坐标,则得ND的值,由S△NBC=S△NDC+S△NDB=![]() ×5×ND得S△NBC关于x的二次函数,便可求得最大值.
×5×ND得S△NBC关于x的二次函数,便可求得最大值.
解:(1)∵抛物线的解析式为y=-![]() [(x-2)2+n]=-
[(x-2)2+n]=-![]() (x-2)2-
(x-2)2-![]() n,∴抛物线的对称轴为直线x=2.∵点A和点B关于直线x=2对称,∴
n,∴抛物线的对称轴为直线x=2.∵点A和点B关于直线x=2对称,∴![]() =2,解得m=1,∴点A的坐标为(-1,0),点B的坐标为(5,0).把A(-1,0)代入y=-
=2,解得m=1,∴点A的坐标为(-1,0),点B的坐标为(5,0).把A(-1,0)代入y=-![]() [(x-2)2+n]得9+n=0,解得n=-9.
[(x-2)2+n]得9+n=0,解得n=-9.
(2)过点N作ND∥y轴交BC于D.由(1)可得抛物线的解析式为y=-![]() [(x-2)2-9]=-
[(x-2)2-9]=-![]() x2+
x2+![]() x+3.当x=0时,y=3,则点C的坐标为(0,3).设直线BC的解析式为y=kx+b,把B(5,0),C(0,3)代入y=kx+b得
x+3.当x=0时,y=3,则点C的坐标为(0,3).设直线BC的解析式为y=kx+b,把B(5,0),C(0,3)代入y=kx+b得![]() ,解得
,解得 .∴直线BC的解析式为y=-
.∴直线BC的解析式为y=-![]() x+3.设点N的坐标为(x,-
x+3.设点N的坐标为(x,-![]() x2+
x2+![]() x+3),则点D的坐标为(x,-
x+3),则点D的坐标为(x,-![]() x+3),∴ND=-
x+3),∴ND=-![]() x2+
x2+![]() x+3-(-
x+3-(-![]() x+3)=-
x+3)=-![]() x2+3x,∴S△NBC=S△NDC+S△NDB=
x2+3x,∴S△NBC=S△NDC+S△NDB=![]() ×5×ND=
×5×ND=![]() (-
(-![]() x2+3x)=-
x2+3x)=-![]() x2+
x2+![]() x=-
x=-![]()
![]() +
+![]() ,当x=
,当x=![]() 时,△NBC面积最大,最大值为
时,△NBC面积最大,最大值为![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案