题目内容
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+4x﹣3的“旋转函数”.小明是这样思考的:由函数y=﹣x2+4x﹣3可知,a1=﹣1,b1=4,c1=﹣3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
(1)请参考小明的方法写出函数y=﹣x2+4x﹣3的“旋转函数”;
(2)若函数![]() 与y=x2﹣3nx+n互为“旋转函数”,求
与y=x2﹣3nx+n互为“旋转函数”,求![]() .
.
【答案】(1)y=x2+4x+3;(2)-1.
【解析】试题分析:(1)根据a1+a2=0,b1=b2,c1+c2=0,求出a2=﹣1,b2=﹣3,c2=﹣2,从而求出函数y=x2﹣3x﹣2的“旋转函数”;
(2)根据旋转函数的定义得到: 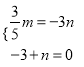 ,从而解得m=﹣15,n=3,进而求出结论.
,从而解得m=﹣15,n=3,进而求出结论.
试题解析:解:(1)在y=﹣x2+4x﹣3中,a1=﹣1,b1=4,c1=﹣3.∵a1+a2=0,b1=b2,c1+c2=0,∴a2=1,b2=4,c2=3,可得函数y=﹣x2+4x﹣3的“旋转函数”为y=x2+4x+3;
(2)根据题意得: 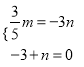 ,解得:
,解得: ![]() .
.
![]() =[
=[![]() ×(﹣15)+3]2017=﹣1.
×(﹣15)+3]2017=﹣1.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目