题目内容
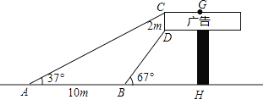
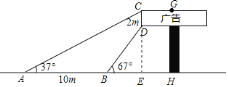
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB=10m,请你根据以上数据计算GH的长.(参考数据tan67°![]() , tan37°
, tan37°![]() )
)
【答案】GH的长为10m.
【解析】
延长CD交AH于点E,则CE⊥AH,设DE=xm,则CE=(x+2)m,通过解直角三角形可得出AE=![]() ,BE=
,BE=![]() ,结合AE-BE=10可得出关于x的方程,解之即可得出x的值,再将其代入GH=CE=CD+DE中即可求出结论.
,结合AE-BE=10可得出关于x的方程,解之即可得出x的值,再将其代入GH=CE=CD+DE中即可求出结论.
解:延长CD交AH于点E,则CE⊥AH,如图所示.
设DE=xm,则CE=(x+2)m,
在Rt△AEC和Rt△BED中,tan37°=![]() ,tan67°=
,tan67°=![]() ,
,
∴AE=![]() ,BE=
,BE=![]() .
.
∵AE﹣BE=AB,tan67°![]() , tan37°
, tan37°![]()
∴![]() ﹣
﹣![]() =10,
=10,
即![]() ﹣
﹣![]() =10,解得:x=8,
=10,解得:x=8,
∴DE=8m,
∴GH=CE=CD+DE=2m+8m=10m.
答:GH的长为10m.

练习册系列答案
相关题目