题目内容
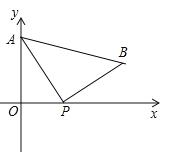
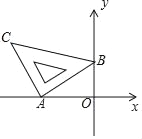
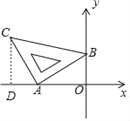
【题目】如图，将含45°角的直角三角尺放置在平面直角坐标系中，其中A（﹣2，0），B（0，1），则直线BC的函数表达式为_____．
【答案】y=﹣
x+1
【解析】分析：
如下图，过点C作CD⊥x轴于点D，然后证△ACD≌△BAO，由此结合已知条件即可求得点B和点C的坐标，这样用“待定系数法”即可求得BC的解析式了.
详解：
如图，过C作CD⊥x轴于点D，
∵∠CAB=90°，
∴∠DAC+∠BAO=∠BAO+∠ABO=90°，
∴∠DAC=∠ABO，
在△AOB和△CDA中：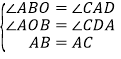
，
∴△AOB≌△CDA（AAS），
∵A（﹣2，0），B（0，1），
∴AD=BO=1，CD=AO=2，
∴C（﹣3，2），
设直线BC解析式为y=kx+b，
∴
，解得：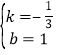
，
∴直线BC的解析式为：
.
故答案为：.
练习册系列答案
相关题目
