题目内容
【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
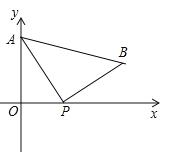
(1)若AB//x轴,求t的值;
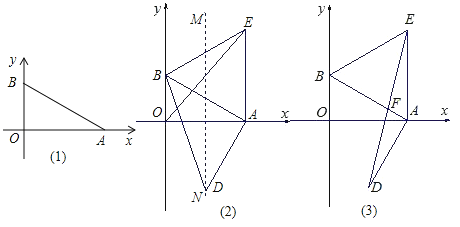
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
【答案】(1)4;(2) (4,7)或(10,-1)或(6,-4)或(0,4).
【解析】
(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;
(2)由全等三角形的性质和等腰三角形的性质可得出结论,注意分类讨论.
解:(1)过点B作BC⊥x轴于点C,如图所示.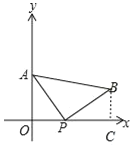
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°-∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
∴t=4÷1=4(秒),
故t的值为4.
(2)当t=3时,OP=3.
∵OA=4,
∴由勾股定理,得
AP=![]() =5.
=5.
∴AP=PB=5,AB=5![]() ,
,
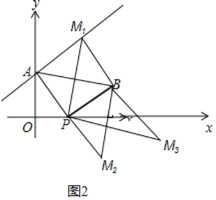
∴当△MPB≌△ABP时,此时四边形APBM1是正方形,四边形APBM3是平行四边形,易得M1(4,7)、M3(10,-1);
当△MPB≌△APB时,此时点M2与点A关于点P对称,易得M2(6,-4).
当两个三角形重合时,此时符合条件的点M的坐标是(0,4);
综上所述,点M的坐标为(4,7)或(10,-1)或(6,-4)或(0,4);

【题目】为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
用水量 | 单价 |
单价不超过 | 2元 |
超过 | 4元 |
超出 |
|
如:某用户![]() 月份用水
月份用水![]() ,则应缴水费:
,则应缴水费:![]() (元)
(元)
(1)某用户![]() 月用水
月用水![]() 应缴水费____________元;
应缴水费____________元;
(2)已知某用户![]() 月份缴水费
月份缴水费![]() 元,求该用户
元,求该用户![]() 月份的用水量;
月份的用水量;
(3)如果该用户![]() 、
、![]() 月份共用水
月份共用水![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份用水量),共交水费
月份用水量),共交水费![]() 元,则该户居民
元,则该户居民![]() 、
、![]() 月份各用水多少
月份各用水多少![]() ?
?