题目内容
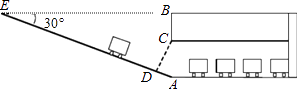
【题目】如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据： 
≈1.414， 
≈1.732）
【答案】解：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．
则DE=BF=CH=10m，
在直角△ADF中，∵AF=80m﹣10m=70m，∠ADF=45°，
∴DF=AF=70m．
在直角△CDE中，∵DE=10m，∠DCE=30°，
∴CE= 
= 
=10 
（m），
∴BC=BE﹣CE=70﹣10 ≈70﹣17.32≈52.7（m）．
答：障碍物B，C两点间的距离约为52.7m．
【解析】通过作垂线把特殊角放在直角三角形中，利用三角函数由边求边，再利用线段之差即可求出BC .
【考点精析】掌握关于仰角俯角问题是解答本题的根本，需要知道仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
练习册系列答案
阅读快车系列答案
相关题目
