题目内容
【题目】如图，已知直角坐标系中，A、B、D三点的坐标分别为A（8，0），B（0，4），D（﹣1，0），点C与点B关于x轴对称，连接AB、AC．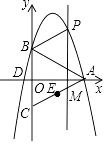
（1）求过A、B、D三点的抛物线的解析式；
（2）有一动点E从原点O出发，以每秒2个单位的速度向右运动，过点E作x轴的垂线，交抛物线于点P，交线段CA于点M，连接PA、PB，设点E运动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S与t的函数关系式，并求出四边形PBCA的最大面积；
（3）抛物线的对称轴上是否存在一点H，使得△ABH是直角三角形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
【答案】
（1）解：∵A（8，0），D（﹣1，0），
设过A、B、D三点的抛物线的解析式为y=a（x+1）（x﹣8），将B（0，4）代入得﹣8a=4，
∴a=﹣ 
，
∴抛物线的解析式为y=﹣ （x+1）（x﹣8）=﹣ x2+ 
x+4；
（2）解：△ABC中，AB=AC，AO⊥BC，则OB=OC=4，
∴C（0，﹣4）．
由A（8，0）、B（0，4），得：直线AB：y=﹣ x+4；
依题意，知：OE=2t，即 E（2t，0）；
∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；
S=S△ABC+S△PAB= ×8×8+ ×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；
∴当t=2时，S有最大值，且最大值为64；
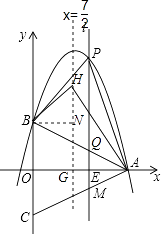
（3）解：存在，
∵抛物线的对称轴为：x= 
= ，
∴设H（ ，m），
∵A（8，0），B（0，4），
∴AH2=（8﹣ ）2+m2= 
+m2，AB2=82+42=80，BH2=（ ）2+（4﹣m）2=m2﹣8m+ 
①当∠ABH=90°时，AH2=BH2+AB2，即 +m2=m2﹣8m+ +80，
解得：m=11，
∴H（ ，11），
②当∠AHB=90°时，AH2+BH2=AB2， +m2+m2﹣8m+ =80，
解得：m=2± 
，
∴H（ ，2+ ），（ ，2﹣ ），
③当∠BAH=90°时，AB2+AH2=HB2，即80+ +m2=m2﹣8m+ ，
解得：m=﹣9，
∴H（ ，﹣9），
综上所述，H（ ，11）或（ ，2+ ）或（ ，2﹣ ）或（ ，﹣9）．
【解析】（1）根据A（8，0），D（-1，0），设过A、B、D三点的抛物线的解析式为y=a（x+1）（x-8），将Ba，进而求得抛物线的解析式；
（2）把四边形PBCA可看作△ABC、△PBA两部分；△ABC的面积是定值，求出△PBA的面积表达式；再求出S、t的函数关系式后，由函数的性质可求得S的最大值；
（3）抛物线的对称轴为再，根据两点间的距离公式分三种情况：①当∠ABH=90°时，②当∠AHB=90°时，③当∠BAH=90°时，根据勾股定理列方程即可得到结论．
