题目内容
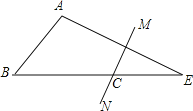
【题目】如图所示,在![]() 中,
中,![]() ,AE的垂直平分线MN交BE于点C,且
,AE的垂直平分线MN交BE于点C,且![]() ,则
,则![]() 的度数是______.
的度数是______.
【答案】![]()
【解析】
首先连接AC,由AE的垂直平分线MN交BE于点C,可得AC=EC,又由AB+BC=BE,易证得AB=AC,然后由等腰三角形的性质与三角形内角和定理,求得∠BAE=∠BAC+∠CAE=180°-4∠E+∠E=105°,继而求得答案.
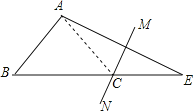
连接AC,
∵MN是AE的垂直平分线,
∴AC=EC,
∴∠CAE=∠E,
∵AB+BC=BE,BC+EC=BE,
∴AB=EC=AC,
∴∠B=∠ACB,
∵∠ACB=∠CAE+∠E=2∠E,
∴∠B=2∠E,
∴∠BAC=180°-∠B-∠ACB=180°-4∠E,
∵∠BAE=∠BAC+∠CAE=180°-4∠E+∠E=105°,
解得:∠E=25°,
∴∠B=2∠E=50°.
故答案为:50°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目