题目内容
【题目】如图，在平面直角坐标系xOy中，B1（0，1），B2（0，3），B3（0，6），B4（0，10），…，以B1B2为对角线作第一个正方形A1B1C1B2，以B2B3为对角线作第二个正方形A2B2C2B3，以B3B4为对角线作第三个正方形A3B3C3B4，…，如果所作正方形的对角线BnBn+1都在y轴上，且BnBn+1的长度依次增加1个单位，顶点An都在第一象限内（n≥1，且n为整数）. 那么A1的坐标为____________；An的坐标为_________（用含n的代数式表示）.
【答案】 （1,2） 
【解析】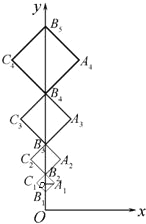
作A1D⊥y轴于点D，
则B1D=B1B2÷2=(31)÷2=1，
A1D=B1D=1，
∴A1的横坐标= A1D=1，A1的纵坐标=B1D+B1O=1+1=
=2，
即A1的坐标=（1,2）
同理可得A2的横坐标=(B2B3)÷2=
，
A2的纵坐标=OB2+(B2B3)÷2=3+(63)÷2=
=4.5，
∴An的横坐标为
，纵坐标为
，
故答案为：(1). （1,2） (2). 
练习册系列答案
小学教材完全解读系列答案
相关题目
