题目内容
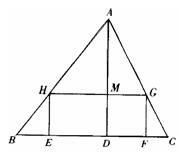
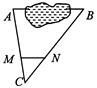
如图,△ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC、AB上,高AD与HG的交点为M.
(1)求证: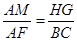 ;
;
(2)求这个矩形EFGH的周长.

(1)求证:
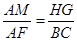 ;
;(2)求这个矩形EFGH的周长.
(1)根据矩形的性质可得EF∥GH,即可证得△AHG∽△ABC,从而得到结论;(2)72cm
试题分析:(1)根据矩形的性质可得EF∥GH,即可证得△AHG∽△ABC,从而得到结论;
(2)由(1)得
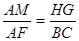 ,设HE=x,则HG=2x,AM=AD-DM=AD-HE=30-x,即可得到关于x的方程,解出x的值,在根据矩形的周长公式求解即可.
,设HE=x,则HG=2x,AM=AD-DM=AD-HE=30-x,即可得到关于x的方程,解出x的值,在根据矩形的周长公式求解即可.(1)∵四边形EFGH为矩形
∴EF∥GH
∴∠AHG=∠ABC
又∵∠HAG=∠BAC
∴△AHG∽△ABC
∴
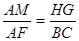 ;
; (2)由(1)得
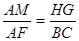 ,设HE=x,则HG=2x,
,设HE=x,则HG=2x,AM=AD-DM=AD-HE=30-x
可得
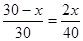
解得x=12,2x="24"
所以矩形EFGH的周长为2×(12+24)=72cm.
点评:相似三角形的应用是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
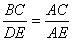
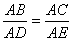
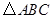 中,
中,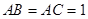 ,
,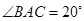 .动点P、Q分别在直线
.动点P、Q分别在直线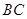 上运动,且始终保持
上运动,且始终保持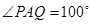 .设
.设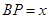 ,
,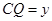 ,则
,则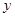 与
与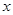 的函数关系的图象大致可以表示为
的函数关系的图象大致可以表示为 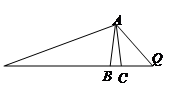
 、
、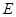 分别是
分别是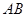 、
、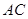 的中点,则
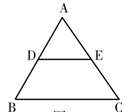
的中点,则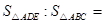 ( )
( )
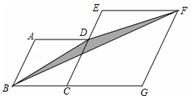
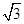 B.4 C.
B.4 C.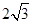 D.
D.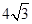
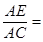 _______.
_______.