题目内容
如图,在直角坐标系xoy中,已知两点O1(3,0)、B(-2,0),⊙O1与x轴交于原点O和点A,E是y轴上的一个动点,设点E的坐标为(0,m).
(1)当点O1到直线BE的距离等于3时,求直线BE的解析式;
(2)当点E在y轴上移动时,直线BE与⊙O1有哪几种位置关系;直接写出每种位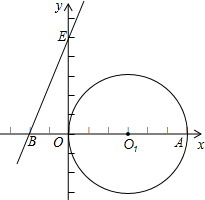 置关系时的m的取值范围;
置关系时的m的取值范围;
(3)若在第(1)题中,设∠EBA=α,求sin2α-2sinα•cosα的值.
解:(1)由已知得BE是⊙O1的切线,
设切点为M,连接O1M,则O1M⊥BM,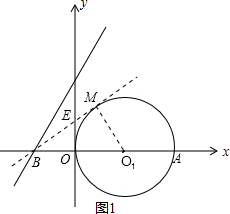
∴O1M=3,BM=4,又OE⊥BO,
∴△BOE∽△BMO,
∴ =
=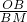 ,
,
∴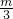 =
=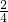 ,
,
∴m= ,
,
设此时直线BE的解析式是y=kx+m,
将B(-2,0)及m= 代入上式,解得k=
代入上式,解得k= ,
,
∴y= x
x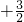 ,
,
由圆的对称性可得:m=- ,直线BE也与⊙O1相切,
,直线BE也与⊙O1相切,
同理可得:y2=- x-
x- ;
;
(2)当m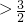 或m<-
或m<- 时,直线与圆相离,
时,直线与圆相离,
当m= 或m=-
或m=- 时,直线与圆相切,
时,直线与圆相切,
当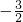 <m<
<m< 时,直线与圆相交;
时,直线与圆相交;
(3)当直线BE与⊙O1相切时,显然存在另一条直线BF也与⊙O1相切,
设直线BE、BF与⊙O1相切于点M、N,连接O1M、O1N,有O1M⊥BM,O1N⊥BN,由圆的对称性可知∠EBF=2∠EBO=2∠α,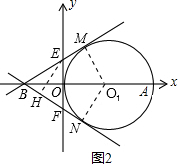
sinα=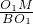 =
= ,
,
cosα=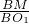 =
= ,
,
过E作EH⊥BF于H,再△BEF中,
由三角形等积性质得;EH•BF=EF•BO,
BF=BE= ,EF=2m=3,BO=2,
,EF=2m=3,BO=2,
∴EH= ,
,
sin2α=sin∠EBF=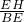 =
=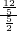 =
=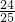 ,
,
由此可得:sin2α-2sinα•cosα=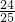
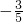 ×
× ×2=0.
×2=0.
分析:(1)由已知得出BE是⊙O1的切线,先设切点为M,连接O1M,则O1M⊥BM,得出O1M、BM的值,再根据OE⊥BO,又得出△BOE∽△BMO,即可求出m的值,最后设出直线BE的解析式是y=kx+m,
把B点的坐标以及m的值代入解出k的值,从而求出直线BE的解析式;
(2)根据(1)所求出的m的值,分三种情况进行讨论,即可得出直线BE与⊙O1的位置关系;
(3)先设直线BE、BF与⊙O1相切,由圆的对称性可知∠EBF=2∠EBO=2∠α,得出sinα与cosα的值,再过E作EH⊥BF于H,由三角形等积性质得出EH•BF=EF•BO,即可求出EH的值,最后即可求出sin2α-2sinα•cosα的值;
点评:此题考查了一次函数的综合;解题的关键是根据直线与圆的位置关系,点到直线的距离以及锐角三角函数的求法分别进行解答.
设切点为M,连接O1M,则O1M⊥BM,

∴O1M=3,BM=4,又OE⊥BO,
∴△BOE∽△BMO,
∴
 =
=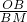 ,
,∴
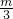 =
=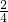 ,
,∴m=
 ,
,设此时直线BE的解析式是y=kx+m,
将B(-2,0)及m=
 代入上式,解得k=
代入上式,解得k= ,
,∴y=
 x
x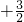 ,
,由圆的对称性可得:m=-
 ,直线BE也与⊙O1相切,
,直线BE也与⊙O1相切,同理可得:y2=-
 x-
x- ;
;(2)当m
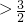 或m<-
或m<- 时,直线与圆相离,
时,直线与圆相离,当m=
 或m=-
或m=- 时,直线与圆相切,
时,直线与圆相切,当
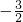 <m<
<m< 时,直线与圆相交;
时,直线与圆相交;(3)当直线BE与⊙O1相切时,显然存在另一条直线BF也与⊙O1相切,
设直线BE、BF与⊙O1相切于点M、N,连接O1M、O1N,有O1M⊥BM,O1N⊥BN,由圆的对称性可知∠EBF=2∠EBO=2∠α,

sinα=
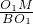 =
= ,
,cosα=
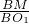 =
= ,
,过E作EH⊥BF于H,再△BEF中,
由三角形等积性质得;EH•BF=EF•BO,
BF=BE=
 ,EF=2m=3,BO=2,
,EF=2m=3,BO=2,∴EH=
 ,
,sin2α=sin∠EBF=
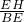 =
=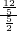 =
=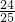 ,
,由此可得:sin2α-2sinα•cosα=
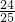
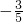 ×
× ×2=0.
×2=0.分析:(1)由已知得出BE是⊙O1的切线,先设切点为M,连接O1M,则O1M⊥BM,得出O1M、BM的值,再根据OE⊥BO,又得出△BOE∽△BMO,即可求出m的值,最后设出直线BE的解析式是y=kx+m,
把B点的坐标以及m的值代入解出k的值,从而求出直线BE的解析式;
(2)根据(1)所求出的m的值,分三种情况进行讨论,即可得出直线BE与⊙O1的位置关系;
(3)先设直线BE、BF与⊙O1相切,由圆的对称性可知∠EBF=2∠EBO=2∠α,得出sinα与cosα的值,再过E作EH⊥BF于H,由三角形等积性质得出EH•BF=EF•BO,即可求出EH的值,最后即可求出sin2α-2sinα•cosα的值;
点评:此题考查了一次函数的综合;解题的关键是根据直线与圆的位置关系,点到直线的距离以及锐角三角函数的求法分别进行解答.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
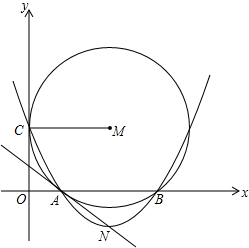 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.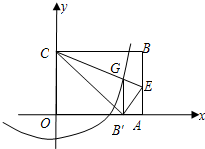 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.