题目内容
【题目】已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.
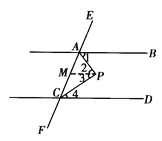
解:过P点作PM∥AB交AC于点M.
∵AB∥CD, ( )
∴∠BAC+∠ACD=180°. ( )
∵PM∥AB,
∴∠1=∠_______, ( )
且PM∥_______.(平行于同一直线的两直线也互相平行)
∴∠3=∠______. ( )
∵AP平分∠BAC,CP平分∠ACD, ( )
![]() BAC,
BAC, ![]() ACD.
ACD.
![]() .
.
∴∠APC=∠2+∠3=∠1+∠4=90°.
总结:两直线平行时,同旁内角的角平分线______.
【答案】答案见解析.
【解析】试题分析:根据已知和平行线的性质进行推理填空即可.
试题解析:
过P点作PM∥AB交AC于点M.
∵AB∥CD, ( 已知 )
∴∠BAC+∠ACD=180°. ( 两直线平行,同旁内角互补 )
∵PM∥AB,
∴∠1=∠_2 , ( 两直线平行,内错角相等 )
且PM∥__CD__.(平行于同一直线的两直线也互相平行)
∴∠3=∠__4__. ( 两直线平行,内错角相等 )
∵AP平分∠BAC,CP平分∠ACD, ( 已知 )
![]() BAC,
BAC, ![]() ACD.
ACD.
![]() .
.
∴∠APC=∠2+∠3=∠1+∠4=90°.

练习册系列答案
相关题目