题目内容
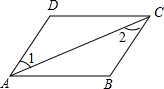已知：如图，在四边形ABCD中，AC是对角线，AD=BC，∠1=∠2．求证：AB=CD．
分析：根据条件可以利用SAS证明△ADC≌△CBA，再根据全等三角形对应边相等可证出结论．
解答：证明：在△ADC和△CBA中：
，
∴△ADC≌△CBA（SAS），
∴AB=CD．
|
∴△ADC≌△CBA（SAS），
∴AB=CD．
点评：此题主要考查了全等三角形的判定与性质，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
39、已知：如图，在四边形ABCD中，AB=DC，AD=BC，点E在BC上，点F在AD上，AF=CE，EF与对角线BD相交于点O．求证：O是BD的中点．
已知：如图，在四边形ABCD中，AD∥BC，AC⊥BC，点E、F分别是边AB、CD的中点，AF=CE．求证：AD=BC．
已知：如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2．
已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．