题目内容
 已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.
分析:连接AC,作GN∥AD交AC于G,连接MG,根据中位线定理证明MG∥BC,且GM=
BC,根据AD=BC证明GM=GN,可得∠GNM=∠GMN,根据平行线性质可得:∠GMF=∠F,∠GNM=∠DEN从而得出∠DEN=∠F.
| 1 |
| 2 |
解答: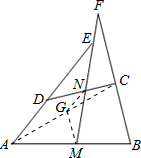 证明:连接AC,作GN∥AD交AC于G,连接MG.
证明:连接AC,作GN∥AD交AC于G,连接MG.
∵N是CD的中点,且NG∥AD,
∴NG=
AD,G是AC的中点,
又∵M是AB的中点,
∴MG∥BC,且MG=
BC.
∵AD=BC,
∴NG=GM,
△GNM为等腰三角形,
∴∠GNM=∠GMN,
∵GM∥BF,
∴∠GMF=∠F,
∵GN∥AD,
∴∠GNM=∠DEN,
∴∠DEN=∠F.
 证明:连接AC,作GN∥AD交AC于G,连接MG.
证明:连接AC,作GN∥AD交AC于G,连接MG.∵N是CD的中点,且NG∥AD,
∴NG=
| 1 |
| 2 |
又∵M是AB的中点,
∴MG∥BC,且MG=
| 1 |
| 2 |
∵AD=BC,
∴NG=GM,
△GNM为等腰三角形,
∴∠GNM=∠GMN,
∵GM∥BF,
∴∠GMF=∠F,
∵GN∥AD,
∴∠GNM=∠DEN,
∴∠DEN=∠F.
点评:此题主要考查平行线性质,以及三角形中位线定理,关键是证明△GNM为等腰三角形.

练习册系列答案
相关题目
 39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
 已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC.
已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC. 已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.