题目内容
 已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
分析:(1)根据勾股定理AB2+BC2=AC2,得出AB2+BC2=2AB2,进而得出AB=BC;
(2)首先证明CDEF是矩形,再根据△BAE≌△CBF,得出AE=BF,进而证明结论.
(2)首先证明CDEF是矩形,再根据△BAE≌△CBF,得出AE=BF,进而证明结论.
解答: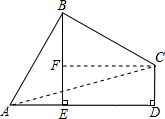 证明:(1)连接AC.
证明:(1)连接AC.
∵∠ABC=90°,
∴AB2+BC2=AC2.
∵CD⊥AD,
∴AD2+CD2=AC2.
∵AD2+CD2=2AB2,
∴AB2+BC2=2AB2,
∴BC2=AB2,
∵AB>0,BC>0,
∴AB=BC.
(2)过C作CF⊥BE于F.
∵BE⊥AD,CF⊥BE,CD⊥AD,
∴∠FED=∠CFE=∠D=90°,
∴四边形CDEF是矩形.
∴CD=EF.
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
∴在△BAE与△CBF中
∴
,
∴△BAE≌△CBF.(AAS)
∴AE=BF.
∴BE=BF+EF=AE+CD.
 证明:(1)连接AC.
证明:(1)连接AC.∵∠ABC=90°,
∴AB2+BC2=AC2.
∵CD⊥AD,
∴AD2+CD2=AC2.
∵AD2+CD2=2AB2,
∴AB2+BC2=2AB2,
∴BC2=AB2,
∵AB>0,BC>0,
∴AB=BC.
(2)过C作CF⊥BE于F.
∵BE⊥AD,CF⊥BE,CD⊥AD,
∴∠FED=∠CFE=∠D=90°,
∴四边形CDEF是矩形.
∴CD=EF.
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
∴在△BAE与△CBF中
∴
|
∴△BAE≌△CBF.(AAS)
∴AE=BF.
∴BE=BF+EF=AE+CD.
点评:此题主要考查了勾股定理的应用以及三角形的全等证明,根据已知得出四边形CDEF是矩形以及△BAE≌△CBF是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
 已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC.
已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC. 已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.