题目内容
39、已知：如图，在四边形ABCD中，AB=DC，AD=BC，点E在BC上，点F在AD上，AF=CE，EF与对角线BD相交于点O．求证：O是BD的中点．分析：由已知条件容易证得四边形FBED是平行四边形，根据平行四边形的性质可证，EF与BD互相平分，所以O是BD的中点．
解答：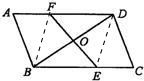
证明：连接FB、DE，
∵AB=DC，AD=BC，
∴四边形ABCD是平行四边形．
∴FD∥BE．
又∵AD=BC，AF=CE，
∴FD=BE．
∴四边形FBED是平行四边形．
∴BO=OD．
即O是BD的中点．
证明：连接FB、DE，∵AB=DC，AD=BC，
∴四边形ABCD是平行四边形．
∴FD∥BE．
又∵AD=BC，AF=CE，
∴FD=BE．
∴四边形FBED是平行四边形．
∴BO=OD．
即O是BD的中点．
点评：平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法，一组对边平行且相等的四边形是平行四边形是最判定平行四边形常用的方法之一，一定要反复训练，熟练掌握．
练习册系列答案
相关题目
已知：如图，在四边形ABCD中，AD∥BC，AC⊥BC，点E、F分别是边AB、CD的中点，AF=CE．求证：AD=BC．
已知：如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2．
已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．