题目内容
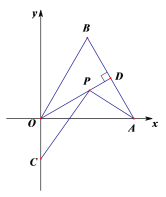
【题目】如图,在平面直角坐标系中,![]() OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是![]() ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.
【答案】![]()
【解析】
由题意知,点A与点B关于直线OD对称,连接BC,则BC的长即为PC+AP的最小值,过点B作BN⊥y轴,垂足为N,过B作BM⊥x轴于M,求出BN、CN的长,然后利用勾股定理进行求解即可.
由题意知,点A与点B关于直线OD对称,连接BC,则BC的长即为PC+AP的最小值,
过点B作BN⊥y轴,垂足为N,过B作BM⊥x轴于M,则四边形OMBN是矩形,
∵△ABO是等边三角形,
∴OM=![]() AO=
AO=![]() ×4=2,∴BN=OM=2,
×4=2,∴BN=OM=2,
在Rt△OBM中,BM=![]() =
=![]() =2
=2![]() ,
,
∴ON=BM=2![]() ,
,
∵C![]() ,
,
∴CN=ON+OC=2![]() +
+![]() =3
=3![]() ,
,
在Rt△BNC中,BC=![]() ,
,
即PC+AP的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目