题目内容
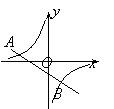
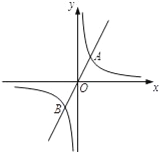
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于点A、B,AB=2
的图象交于点A、B,AB=2![]() ,
,
(1)求k的值;
(2)若反比例函数y=![]() 的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
【答案】(1)k=2(2)当△ABC为直角三角形,点C的坐标为(﹣4,﹣![]() )、(4,
)、(4,![]() )、(﹣2,﹣1)或(2,1)
)、(﹣2,﹣1)或(2,1)
【解析】分析:(1)过点A作AD⊥x轴,垂足为D,由点A、B的对称性可求出OA的值,根据点在直线上,设点A的坐标为(a,2a),在Rt△OAD中,通过勾股定理即可求出A的坐标,由点A的坐标利用待定系数法即可求出结论;
(2)由点A、B的对称性,结合点A的坐标求出点B的坐标,根据点C在反比例函数上,设出点C的坐标为(n,![]() ),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
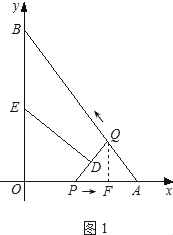
详解:(1)过点A作AD⊥x轴,垂足为D,如图1所示.
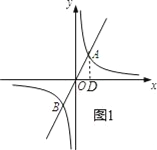
由题意可知点A与点B关于点O中心对称,且AB=2![]() ,∴OA=OB=
,∴OA=OB=![]() .
.
设点A的坐标为(a,2a),在Rt△OAD中,∠ADO=90°,由勾股定理得:
a2+(2a)2=(![]() )2,解得:a=1,∴点A的坐标为(1,2).
)2,解得:a=1,∴点A的坐标为(1,2).
把A(1,2)代入y=![]() 中得:2=
中得:2=![]() ,解得:k=2.
,解得:k=2.
(2)∵点A的坐标为(1,2),点A、B关于原点O中心对称,
∴点B的坐标为(﹣1,﹣2).设点C的坐标为(n,![]() ),
),
△ABC为直角三角形分三种情况:
①∠ABC=90°,则有AB⊥BC,![]() =﹣1,即n2+5n+4,
=﹣1,即n2+5n+4,
解得:n1=﹣4,n2=﹣1(舍去),此时点C的坐标为(﹣4,﹣![]() );
);
②∠BAC=90°,则有BA⊥AC,![]() =﹣1,即n2﹣5n+4=0,
=﹣1,即n2﹣5n+4=0,
解得:n3=4,n4=1(舍去),此时点C的坐标为(4,![]() );
);
③∠ACB=90°,则有AC⊥BC,![]() =﹣1,即n2=4,解得:n5=﹣2,n6=2,
=﹣1,即n2=4,解得:n5=﹣2,n6=2,
此时点C的坐标为(﹣2,﹣1)或(2,1).综上所述:当△ABC为直角三角形,点C的坐标为(﹣4,﹣![]() )、(4,
)、(4,![]() )、(﹣2,﹣1)或(2,1).
)、(﹣2,﹣1)或(2,1).

 寒假学与练系列答案
寒假学与练系列答案【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70,100 | 85 | 100 |
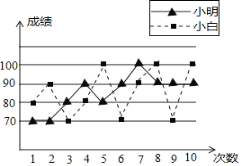
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由