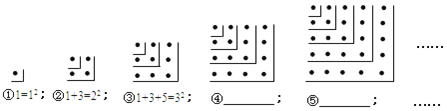
题目内容
【题目】如图,已知点A的坐标为(a,6)(其中a<-![]() ),射线OA与反比例函数
),射线OA与反比例函数![]() 的图像交于点P,点B,C分别在函数
的图像交于点P,点B,C分别在函数![]() 的图像上,且AB∥x轴,AC∥y轴,连接BP,CP.
的图像上,且AB∥x轴,AC∥y轴,连接BP,CP.
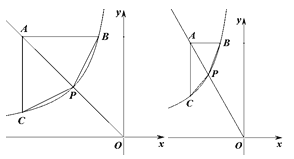
(1)当a=-6时.①求点P的坐标;②求△ABP的面积S△ABP和△ACP的面积S△ACP.
(2)当a<-![]() 时,随着a的值变化,猜想
时,随着a的值变化,猜想![]() 的值是否变化,若变化说明理由,若不变,求出结果.
的值是否变化,若变化说明理由,若不变,求出结果.
【答案】(1)①点P的坐标是(﹣3,3),②△ABP的面积S△ABP=![]() ,△ACP的面积S△ACP=
,△ACP的面积S△ACP=![]() (2)不变,
(2)不变,![]() =1.
=1.
【解析】
(1) 当a=﹣6时,确定A点的坐标,根据A、B两点求出直线OA的表达式y=﹣x,
所以能求出点B的坐标和点C 的坐标,根据坐标与图形的性质求出各三角形的面积.
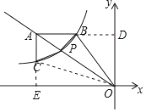
(2) ![]() =1的值不变,理由为:如图2,延长AB交y轴于点D,延长AC交x轴于点E,连接CO.∵AB∥x轴,AC∥y轴,,根据A坐标表示出直线OC解析式,进而表示出D坐标,以及B坐标,得到四边形ABCD为矩形,进而得到BE=CF,利用同底等高三角形面积相等即可求出所求之比.
=1的值不变,理由为:如图2,延长AB交y轴于点D,延长AC交x轴于点E,连接CO.∵AB∥x轴,AC∥y轴,,根据A坐标表示出直线OC解析式,进而表示出D坐标,以及B坐标,得到四边形ABCD为矩形,进而得到BE=CF,利用同底等高三角形面积相等即可求出所求之比.
解:(1)当a=﹣6时,A的坐标为(﹣6,6),射线OA所在的直线是:y=﹣x,
点B的坐标(﹣![]() ,6),点C的坐标(﹣6,
,6),点C的坐标(﹣6,![]() ).
).
∴①点P的坐标是(﹣3,3);
②△ABP的面积S△ABP=![]() ;
;
△ACP的面积S△ACP=![]() .
.
(2)不变
![]() =1.
=1.
理由:延长AB交y轴于点D,延长AC交x轴于点E,连接CO.
∵AB∥x轴,AC∥y轴,∴四边形AEOD为平行四边形.
又∵∠DOE=90°,∴平行四边形AEOD为矩形.∴S△AEO=S△ADO.
又∵S△CEO=S△BDO=![]() ,∴S△ACO=S△ABO.
,∴S△ACO=S△ABO.
又∵S△ACP=![]() ×S△ACO,S△ABP=
×S△ACO,S△ABP=![]() ×S△ABO,
×S△ABO,
∴S△ACP=S△ABP.∴![]() =1.
=1.

【题目】我国是水资源比较贫乏的国家之一,为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段来达到节约用水的目的,规定如下用水收费标准:每户每月的用水不超过20立方米(含20立方米)时,水费按“基本价”收费:超过20立方米时,不超过的部分仍按“基本价”收费,超过部分按“调节价”收费.某户居民今年4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
4 | 20 | 42 |
5 | 24 | 56.40 |
(1)请你算一算该市水费的“调节价”每立方米多少元?
(2)若该户居民6月份用水量为30立方米,请算一算,6月份水费是多少元?