题目内容
【题目】观察下面的点阵图和相应的等式，探究其中的规律：
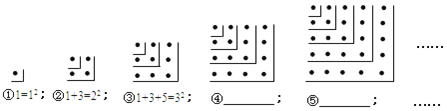
（1）在④和⑤后面的横线上分别写出相应的等式；
（2）试用含有n的式子表示第n个等式： ；（n为正整数）
（3）请用上述规律计算：
①1+3+5+…+49；
②101+103+105+…+197+199．
【答案】（1）1+3+5+7=4
，1+3+5+7+9=5 （2）1+3+5+7......+(2n-1)=n （3）①625，②7500
【解析】
根据图示和数据可知规律是：等式左边是连续的奇数和，等式右边是等式左边的首数与末数的平均数的平方，据此规律即可解答（1）、（2）和（3）①，对于（3）②，可进行下面的变形：101+103+105+…+197+199＝（1+3+5+…+199）﹣（1+3+5+…+99），再利用规律计算.
解：（1）由图①知黑点个数为1个，由图②知在图①的基础上增加3个，由图③知在图②基础上增加5个，则可推知图④应为在图③基础上增加7个即有1+3+5+7＝42，图⑤应为1+3+5+7+9＝52．
（2）由（1）中推理可知第n个图形黑点个数为：1+3+5+…+（2n﹣1）＝n2；
故第n个等式为：1+3+5+…+（2n﹣1）＝n2；
（3）①由（1）中的推理可知1+3+5+…+49＝252＝625；
②101+103+105+…+197+199＝（1+3+5+…+199）﹣（1+3+5+…+99）＝1002﹣502＝7500.
练习册系列答案
阅读快车系列答案
相关题目
