题目内容
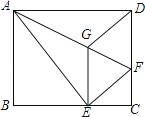
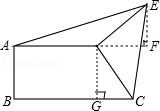
【题目】已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )

A.1 B.2 C.5 D.无法确定
【答案】A
【解析】
试题分析:因为知道AD的长,所以只要求出AD边上的高,就可以求出△ADE的面积.过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,构造出Rt△EDF≌Rt△CDG,求出GC的长,即为EF的长,然后利用三角形的面积公式解答即可.
解:过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
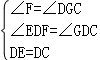 ,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选A.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目