题目内容
如图,正方形桌面ABCD,面积为2,铺一块桌布EFGH,点A、B、C、D分别是EF、FG2、GH、HE的中点,则桌布EFGH的面积是( )
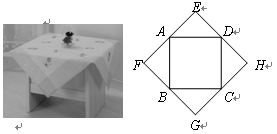

| A.2 | B.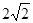 | C.4 | D.8 |
D
易得正方形ABCD的边长,进而利用勾股定理求得正方形EFGH的边长,即可求得相
应的面积。
解:连接EG,
∵正方形桌面ABCD,面积为2,
∴AD=AB= ,
,
又∵A、B是EF,FG的中点,
∴EG=2 ,
,
∵四边形ABCD为正方形,
∴∠F=90°,且EF=FG,
根据勾股定理得:FG2+EF2=EG2,
∴2FG2=EG2,2FG2=(2 )2,
)2,
∴FG=2,
∴桌布EFGH的面积是FG2=2×2=4,
故选C.
应的面积。

解:连接EG,
∵正方形桌面ABCD,面积为2,
∴AD=AB=
 ,
,又∵A、B是EF,FG的中点,
∴EG=2
 ,
,∵四边形ABCD为正方形,
∴∠F=90°,且EF=FG,
根据勾股定理得:FG2+EF2=EG2,
∴2FG2=EG2,2FG2=(2
 )2,
)2,∴FG=2,
∴桌布EFGH的面积是FG2=2×2=4,
故选C.

练习册系列答案
相关题目

 ( )
( ) 
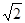 B.
B.  C.
C.  D.
D.
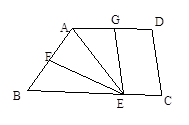
 ,则AE= ( )
,则AE= ( )
 B.
B.  C.
C. D.2
D.2



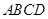 中,
中,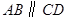 ,
,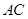 平分
平分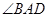 ,
,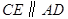 交
交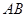 于
于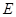 .
.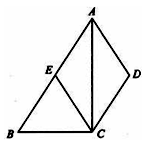
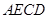 是菱形;
是菱形;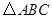 的形状,并说明理由.
的形状,并说明理由.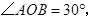 过
过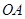 上到点
上到点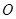 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作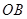 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为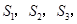 ….则
….则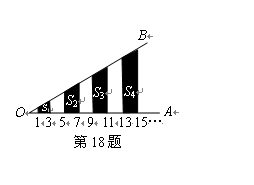
 ;
;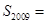 .
.