题目内容
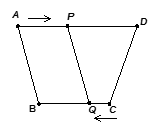
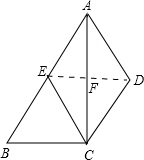
(本小题满分7分)如图,四边形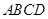 中,
中,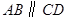 ,
,
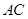 平分
平分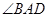 ,
,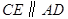 交
交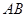 于
于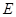 .
.
小题1:(1)求证:四边形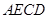 是菱形;
是菱形;
小题2:(2)若点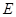 是
是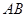 的中点,试判断
的中点,试判断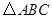 的形状,并说明理由.
的形状,并说明理由.
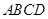 中,
中,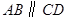 ,
,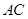 平分
平分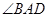 ,
,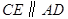 交
交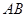 于
于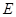 .
.
小题1:(1)求证:四边形
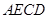 是菱形;
是菱形;小题2:(2)若点
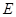 是
是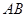 的中点,试判断
的中点,试判断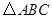 的形状,并说明理由.
的形状,并说明理由.小题1:(1)
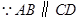 ,即
,即 ,又
,又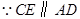 ,
,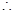 四边形
四边形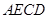 是平行四边形.
是平行四边形.(2分)
 平分
平分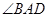 ,
,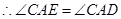 , (3分)
, (3分)又
 ,
,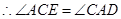 ,
,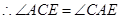 ,
,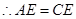 ,
,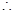 四边形
四边形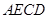 是菱形.
是菱形.小题2:(2)证法一:
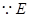 是
是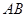 中点,
中点,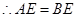 .
.又
 ,
,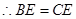 ,
,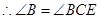 , (5分)
, (5分)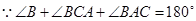 , (6分)
, (6分)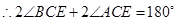 ,
,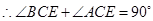 .
.即
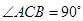 ,
,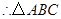 是直角三角形. (7分)
是直角三角形. (7分)证法二:连
 ,则
,则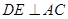 ,且平分
,且平分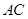 , (5分)
, (5分)设
 交
交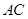 于
于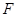 .
.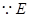 是
是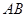 的中点,
的中点,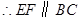 .(6分)
.(6分)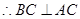 ,
,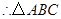 是直角三角形.
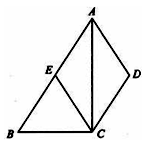
是直角三角形.分析:(1)根据两组对边分别平行证得四边形AECD是平行四边形,只需证明四边形AECD的两邻边相等即可.根据AC平分∠BAD,以及CE∥AD,易证得∠EAC=∠ECA,由此可知AE=CE,即四边形AECD是菱形;
(2)连DE,DE交AC于F,根据菱形的性质,对角线互相垂直且平分有:DE垂直平分AC,则EF是△ABC的中位线,有EF∥BC,则BC⊥AC,由此可证得△ABC是直角三角形.
解答:(1)证明:∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四边形AECD是平行四边形.
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四边形AECD是菱形;
(2)解:△ABC是直角三角形.
证法一:∵E是AB中点,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,
∴△ABC是直角三角形.
证法二:连DE,由四边形AECD是菱形,得到DE⊥AC,且平分AC,
设DE交AC于F,
∵E是AB的中点,且F为AC中点,
∴EF∥BC.∠AFE=90°,
∴∠ACB=∠AFE=90°,
∴BC⊥AC,
∴△ABC是直角三角形.
(2)连DE,DE交AC于F,根据菱形的性质,对角线互相垂直且平分有:DE垂直平分AC,则EF是△ABC的中位线,有EF∥BC,则BC⊥AC,由此可证得△ABC是直角三角形.

解答:(1)证明:∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四边形AECD是平行四边形.
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四边形AECD是菱形;
(2)解:△ABC是直角三角形.
证法一:∵E是AB中点,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,
∴△ABC是直角三角形.
证法二:连DE,由四边形AECD是菱形,得到DE⊥AC,且平分AC,
设DE交AC于F,
∵E是AB的中点,且F为AC中点,
∴EF∥BC.∠AFE=90°,
∴∠ACB=∠AFE=90°,
∴BC⊥AC,
∴△ABC是直角三角形.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
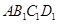 的边长为1,
的边长为1,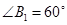 ;作
;作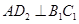 于点
于点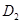 ,以
,以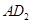 为一边,做第二个菱形
为一边,做第二个菱形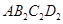 ,使
,使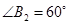 ;作
;作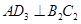 于点
于点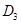 ,以
,以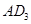 为一边做第三个菱形
为一边做第三个菱形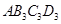 ,使
,使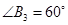 ;
;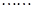 依此类推,这样做的第
依此类推,这样做的第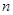 个菱形
个菱形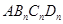 的边
的边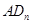 的长是 .
的长是 .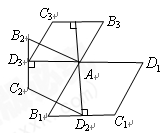
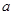 cm,其中矩形的长是宽的2倍,那么它们的面积
cm,其中矩形的长是宽的2倍,那么它们的面积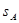 、
、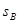 、
、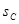 之间的关系式正确的是( ).
之间的关系式正确的是( ).