Question

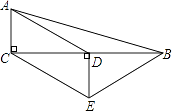
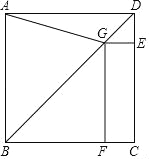
【题目】如图，已知二次函数的图象经过三点.

（1）求该二次函数的解析式；

（2）点是该二次函数图象上的一点，且满足(是坐标原点)，求点的坐标；

（3）点是该二次函数图象上位于一象限上的一动点，连接分别交轴与点若的面积分别为求的最大值.

Answer 1

【答案】（1）；（2）满足条件的点有：；（3）当时，有最大值，最大值为：.

【解析】

试题分析：（1）利用待定系数法求得二次函数的解析式即可；（2）设直线与轴的交点为，根据已知条件求得t=±8，根据t的值求得直线BD的解析式，把直线BD的解析式与抛物线的解析式联立组成方程组，解方程组即可求得点D的坐标；（3）过点P作PH//轴交直线于点，设，则，所以，分别用t表示出的面积分别为在计算出与t的函数关系，利用二次函数的性质求解即可.=

试题解析：

（1）由题意得：设抛物线的解析式为：；

因为抛物线图像过点,

解得

所以抛物线的解析式为：

即：

(2)设直线与轴的交点为

当时，直线解析式为：

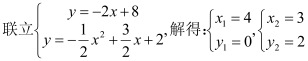
所以，点

当时，直线解析式为：

所以，点

综上：满足条件的点有：

（3）：过点P作PH//轴交直线于点，设

BC直线的解析式为 故：

AP直线的解析式为：

故：

；

即：

所以，当时，有最大值，最大值为：.