题目内容
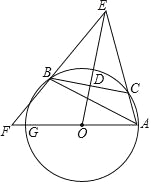
【题目】如图,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() 为
为![]() 的中点,作
的中点,作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
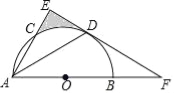
(1)求证:![]() 为半圆
为半圆![]() 的切线;
的切线;
(2)若![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
【答案】(1)证明见解析(2)![]() -6π
-6π
【解析】
试题分析:(1)直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF,即可得出答案;
(2)直接利用得出S△ACD=S△COD,再利用S阴影=S△AED﹣S扇形COD,求出答案.
试题解析:(1)连接OD,
∵D为![]() 的中点,
的中点,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∵DE⊥AC,
∴∠E=90°,
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF为半圆O的切线;
(2)连接OC与CD,
∵DA=DF,
∴∠BAD=∠F,
∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°,
∵OC=OA,
∴△AOC为等边三角形,
∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°,
∴∠DOF=60°,
在Rt△ODF中,DF=6![]() ,
,
∴OD=DFtan30°=6,
在Rt△AED中,DA=6![]() ,∠CAD=30°,
,∠CAD=30°,
∴DE=DAsin30°·![]() ,EA=DAcos30°=9,
,EA=DAcos30°=9,
∵∠COD=180°﹣∠AOC﹣∠DOF=60°,
∴CD∥AB,
故S△ACD=S△COD,
∴S阴影=S△AED﹣S扇形COD=![]() ×9×3
×9×3![]() ﹣
﹣![]() π×62=
π×62=![]() ﹣6π.
﹣6π.
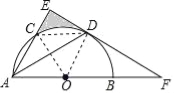

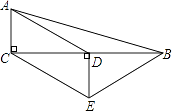
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.