题目内容
【题目】如图,把长方形纸片OABC放入直角坐标系中,使OA, OC分别落在x轴、y轴的正半轴上,连接AC,将![]() 翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E,已知CB=8,AB=4.
翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E,已知CB=8,AB=4.

(1)求AC所在直线的函数关系式;
(2)求点E的坐标和![]() 的面积:
的面积:
(3)求点D的坐标,并判断点(8, -4)是否在直线OD上,说明理由.
【答案】(1) y=![]() ;(2)10;(3) D坐标为(
;(2)10;(3) D坐标为(![]() ),点(8,
),点(8,![]() )在直线OD上,理由见解析;
)在直线OD上,理由见解析;
【解析】
(1)根据已知求得A、C的坐标,然后根据待定系数法即可求解;(2)首先证明△ACE是等腰三角形,在直角△OCE中利用勾股定理即可求得OE的长,求得E的坐标,进而求得△ACE的面积;(3)作DF⊥x轴于点F,根据△ADE的面积求得D的纵坐标,然后在直角△ADF中,利用勾股定理求得AF的长,从而求得OF,即可得到D的坐标,然后利用待定系数法求得直线OD的解析式,然后把点(8,-4)代入判断即可;
解:(1) ∵OA,OC分别落在x轴、y轴的正半轴上,CB=8,AB=4.
∴A(8,0)、C(0,4),
设直线AC解析式为y=kx+b,
∴![]()
解得: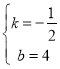
∴AC所在直线的函数关系式为y=![]() ;
;
(2)∵长方形OABC中,BC∥OA,
∴∠BCA=∠CAO,
又∵∠BCA=∠ACD,
∴∠ACD=∠CAO,
∴CE=AE;
设CE=AE=x,则OE=8-x,在直角△OCE中,OC2+OE2=CE2,
则![]() ,
,
解得:x=5;
则OE=8-5=3,
则E(3,0),
∴S△ACE=![]() ×5×4=10;
×5×4=10;
(3)如图,作DF⊥x轴于点F,
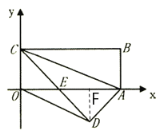
S△ACD=S△ABC=![]() ,
,
∴S△ADE=16-10=6,
又∵S△ADE= ![]() ,
,
∴![]() ×5×DF=6;
×5×DF=6;
∴DF=![]() ,
,
在直角△ADF中,AF=![]() ,
,
则OF=8-![]() ;
;
∴D坐标为(![]() );
);
设直线OD的解析式为y=mx,则![]() ,
,
解得:m=![]() ,
,
则直线OD解析式为:y=![]() x,
x,
当x=8时,y=-4,则(8,![]() )在直线OD上.
)在直线OD上.





