题目内容
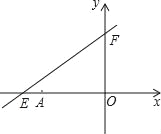
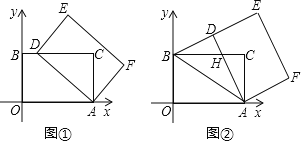
【题目】正方形A1B1C1O,正方形A2B2C2C1,正方形A3B3C3C2,按如图所示的方式放置在平面直角坐标系中,若点A1、A2、A3和C1、C2、C3…分别在直线y=x+1和x轴上,则点B2019的坐标是_____.

【答案】![]() .
.
【解析】
先求得A1(0,1),OA1=1,然后根据正方形的性质求出C1(1,0),B1(1,1),同样的方法求出C2(3,0),B2(3,2),C3(7,0),B3(7,4),……,从而有Cn(2n-1,0),Bm(2n-1,2n-1),由此即可求得答案.
当x=0时,y=x+1=1,
∴A1(0,1),OA1=1,
∵正方形A1B1C1O,
∴A1B1=B1C1=OC1=OA1=1,
∴C1(1,0),B1(1,1),
当x=1时,y=x+1=2,
∴A2(1,2),C1A2=2,
∵正方形A2B2C2C1,
∴A2B2=B2C2=C1C2=C1A1=2,
∴C2(3,0),B2(3,2),
当x=3时,y=x+1=4,
∴A3(3,4),C2A3=4,
∵正方形A3B3C3C2,
∴A3B3=B3C3=C2C3=C2A3=4,
∴C3(7,0),B3(7,4),
……
∴Cn(2n-1,0),Bm(2n-1,2n-1),
∴B2019(22019-1,22018),
故答案为:(22019-1,22018).

【题目】某市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
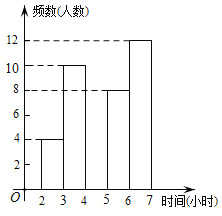
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
【题目】某智能手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
已知A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共90部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?