题目内容
【题目】(1)操究发现:如图1,△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
①求∠EAF的度数;
②DE与EF相等吗?请说明理由
(2)类比探究:如图2,△ABC为等腰直角三角形,∠ACB=90°,点D为AB边上的一点,∠DCE=45°,CF=CD,CF⊥CD,请直接写出下列结果:
①∠EAF的度数
②线段AE,ED,DB之间的数量关系
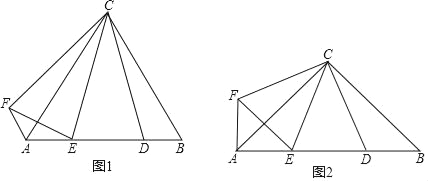
【答案】(1)①120°;②DE=EF;理由见解析;(2)①90°;②AE2+DB2=DE2.
【解析】试题分析:![]() ①证明
①证明![]() ≌
≌![]() ,得到
,得到![]() 即可求得
即可求得![]() 的度数.
的度数.
②证明![]() ≌
≌![]() ,即可得证.
,即可得证.
![]() ①类比
①类比![]() ①的方法即可求得.
①的方法即可求得.
②![]()
试题解析:
(1)①∵![]() 是等边三角形,
是等边三角形,
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,

∴![]() ≌
≌![]() (SAS),
(SAS),
![]()
![]()
②![]() 理由如下:
理由如下:
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,

∴![]() ≌
≌![]() (SAS),
(SAS),
![]()
(2)①∵![]() 是等腰直角三角形,
是等腰直角三角形,![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,

∴![]() ≌
≌![]() (SAS),
(SAS),
![]()
![]()
②![]() 理由如下:
理由如下:
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,

∴![]() ≌
≌![]() (SAS),
(SAS),
![]()
在![]() 中,
中,![]()
又![]()
![]()

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】某市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
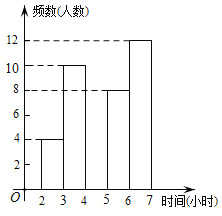
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?