Question

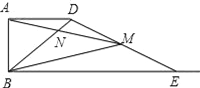
【题目】如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．

(1)求证：△ABD≌△ECB；

(2)若∠DBC＝50°，求∠DCE的度数．

Answer 1

【答案】解： (1)证明：∵ AD∥BC，∴∠ADB＝∠EBC。

∵ 在△ABD和△ECB中 ，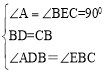

∴△ABD≌△ECB（ASA）。--- -- 3分

（2）∵BC＝BD，∠DBC＝50°，∴∠BCD＝65°。

又∵∠BEC＝90°，∴∠BCE＝40°。

∴∠DCE＝∠BCD－∠BCE＝65°－40°＝25°。

【解析】（1）∵ AD∥BC，∴∠ADB＝∠EBC，再加上BC＝BD，∠A＝90°，CE⊥BD，即可得△ABD≌△ECB；

由BC＝BD根据等边对等角可求出∠BCD，再利用三角形内角和求出∠BCE，即可求到∠DCE。