题目内容
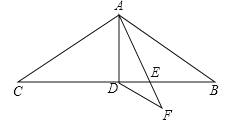
【题目】如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
（1）出发2秒后，求PQ的长；
（2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？
（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．
【答案】（1）28；（2）
；（3）当t为11秒或12秒或13.2秒时，△BCQ为等腰三角形；
【解析】
（1）根据点P、Q的运动速度求出AP，再求出BP和BQ，用勾股定理求得PQ即可；
（2）设出发t秒钟后，△PQB能形成等腰三角形，则BP=BQ，由BQ=2t，BP=8-t，列式求得t即可；
（3）当点Q在边CA上运动时，能使△BCQ成为等腰三角形的运动时间有三种情况：
①当CQ=BQ时，则∠C=∠CBQ，可证明∠A=∠ABQ，则BQ=AQ，则CQ=AQ，从而求得t；
②当CQ=BC时，则BC+CQ=12，易求得t；
③当BC=BQ时，过B点作BE⊥AC于点E，则求出BE，CE，即可得出t．
解:（1）∵BQ=2×2=4（cm），
BP=AB﹣AP=16﹣2×1=14（cm ），
∵∠B=90°，
∴S△PBQ=
；
（2）BQ=2t，BP=16﹣t，
根据题意得：2t=16﹣t，
解得：t=，
即出发秒钟后，△PQB能形成等腰三角形；
（3）①当CQ=BQ时，如图1所示，
则∠C=∠CBQ，
∵∠ABC=90°，
∴∠CBQ+∠ABQ=90°．
∠A+∠C=90°，
∴∠A=∠ABQ，
∴BQ=AQ，
∴CQ=AQ=10，
∴BC+CQ=22，
∴t=22÷2=11秒．
②当CQ=BC时，如图2所示，
则BC+CQ=24，
∴t=24÷2=12秒．
③当BC=BQ时，如图3所示，
过B点作BE⊥AC于点E，
则BE=
=
，
∴CE=
=
=
，
∴CQ=2CE=14.4，
∴BC+CQ=26.4，
∴t=26.4÷2=13.2秒．
综上所述：当t为11秒或12秒或13.2秒时，△BCQ为等腰三角形．
