题目内容
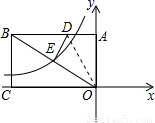
如图，矩形AOCB的两边OC、OA分别位于
轴、
轴上，点B的坐标为B（
），D是AB边上的一点.将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图像上，那么该函数的解析式是 ▲ .
y=
解析:解：过E点作EF⊥OC于F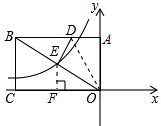 
由条件可知：OE=OA=5，EF /OF =tan∠BOC=BC /OC = 
=3/ 4所以EF=3，OF=4
则E点坐标为（-4，3）
设反比例函数的解析式是y= k/x
则有k=-4×3=-12
∴反比例函数的解析式是y=-12/ x
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图，矩形AOCB的两边OC、OA分别位x轴、y轴上，点B的坐标为B（
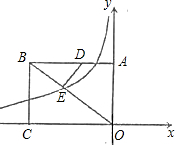如图，矩形AOCB的两边OC、OA分别位于x轴、y轴上，点B的坐标为B（-| 20 |
| 3 |
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
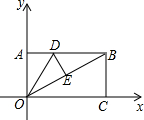如图，矩形AOCB的两边OC、OA分别位于x轴、y轴上，∠ABO=30°，AB=6，D是AB边上的一点，将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在反比例函数y=
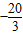，5），D是AB边上的一点．将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图象上，那么该函数的解析式是 ．