题目内容
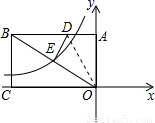
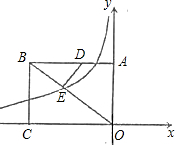如图，矩形AOCB的两边OC、OA分别位于x轴、y轴上，点B的坐标为B（-| 20 |
| 3 |
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
分析：先作EF⊥CO，垂足为点F，连接OD，构造全等三角形，再由勾股定理和相似三角形的性质，求出E点作标，利用待定系数法解答即可．
解答：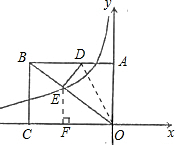
解：作EF⊥CO，垂足为点F，连接OD．
因为点B的坐标为B（-
，5），
所以AB=
，AO=5，
根据折叠不变性，OE=OA=5，
根据勾股定理，OB=
=
，
∵△OEF∽△OBC，
∴
=
，即
=
，
解得：EF=3，
又∵点A的坐标为A（0，5），
∴OF=
=
=4，
∴E点坐标为（-4，3），
设解析式为y=
，
将（-4，3）代入解析式得k=-4×3=-12，
∴解析式为y=-
．
故选D．
解：作EF⊥CO，垂足为点F，连接OD．因为点B的坐标为B（-
| 20 |
| 3 |
所以AB=
| 20 |
| 3 |
根据折叠不变性，OE=OA=5，
根据勾股定理，OB=
52+(
|
| 25 |
| 3 |
∵△OEF∽△OBC，
∴
| EF |
| BC |
| OE |
| OB |
| EF |
| 5 |
| 5 | ||
|
解得：EF=3，
又∵点A的坐标为A（0，5），
∴OF=
| OE2-EF2 |
| 52-32 |
∴E点坐标为（-4，3），
设解析式为y=
| k |
| x |
将（-4，3）代入解析式得k=-4×3=-12，
∴解析式为y=-
| 12 |
| x |
故选D．
点评：此题是一道综合性较强的题目，将翻折变换和用待定系数法求函数解析式结合起来，有一定难度．
练习册系列答案
相关题目
如图，矩形AOCB的两边OC、OA分别位x轴、y轴上，点B的坐标为B（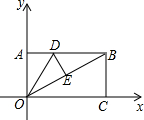
如图，矩形AOCB的两边OC、OA分别位于x轴、y轴上，∠ABO=30°，AB=6，D是AB边上的一点，将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在反比例函数y=
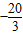，5），D是AB边上的一点．将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图象上，那么该函数的解析式是 ．