题目内容
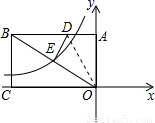
 如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-4,3),D是AB边上的一点,将△ADO沿直线OD翻折,使点A恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是
如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为(-4,3),D是AB边上的一点,将△ADO沿直线OD翻折,使点A恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是y=-
| 108 |
| 25x |
y=-
.| 108 |
| 25x |
分析:首先过E作EF⊥CO,根据B点坐标可得到AO=CB=3,CO=AB=4,再利用勾股定理算出BO的长,然后求出sinα,再根据本折叠的性质可知EO=AO=3,利用三角函数计算出EF的长,再次利用勾股定理计算出FO的长度,进而得到E点坐标,设出反比例函数关系式,利用待定系数法即可求出答案.
解答: 解:过E作EF⊥CO,
解:过E作EF⊥CO,
∵B(-4,3),
∴AO=CB=3,CO=AB=4,
OB=
=5,
sinα=
=
,
∴EF=EO•sinα,
由折叠可得:EO=AO=3,
∴EF=3×
=
,
∴FO=
=
,
∴E(-
,
),
设反比例函数解析式为y=
(k≠0),
则k=-
×
=-
,
故反比例函数解析式为;y=-
,
故答案为:y=-
.
 解:过E作EF⊥CO,
解:过E作EF⊥CO,∵B(-4,3),
∴AO=CB=3,CO=AB=4,
OB=
| CO2+CB2 |
sinα=
| CB |
| BO |
| 3 |
| 5 |
∴EF=EO•sinα,
由折叠可得:EO=AO=3,
∴EF=3×
| 3 |
| 5 |
| 9 |
| 5 |
∴FO=
| EO2-EF2 |
| 12 |
| 5 |
∴E(-
| 12 |
| 5 |
| 9 |
| 5 |
设反比例函数解析式为y=
| k |
| x |
则k=-
| 12 |
| 5 |
| 9 |
| 5 |
| 108 |
| 25 |
故反比例函数解析式为;y=-
| 108 |
| 25x |
故答案为:y=-
| 108 |
| 25x |
点评:此题主要考查了利用待定系数法求反比例函数关系式,折叠的性质,勾股定理,三角函数的应用,解决问题的关键是利用三角函数与勾股定理求出E点坐标.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
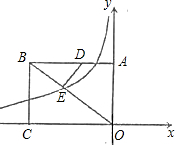 如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(-
如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(-| 20 |
| 3 |
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
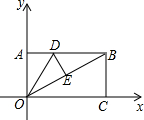 如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,∠ABO=30°,AB=6,D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在反比例函数y=
如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,∠ABO=30°,AB=6,D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在反比例函数y=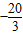 ,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .