题目内容
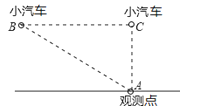
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60![]() 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120![]() 海里。
海里。

(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
【答案】(1)AC=120![]() 海里 ,BC=120
海里 ,BC=120![]() 海里;(2)无触礁危险.
海里;(2)无触礁危险.
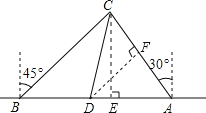
【解析】试题分析:(1)如图所示,过点C作CE⊥AB于点E,可求得∠CBD=45°,∠CAD=60°,设CE=x,在Rt△CBE与Rt△CAE中,分别表示出BE、AE的长度,然后根据AB=60(![]() +
+![]() )海里,代入BE、AE的式子,求出x的值,继而可求出AC、BC的长度;
)海里,代入BE、AE的式子,求出x的值,继而可求出AC、BC的长度;
(2)如图所示,过点D作DF⊥AC于点F,在△ADF中,根据AD的值,利用三角函数的知识求出DF的长度,然后与100比较,进行判断.
试题解析:(1)如图所示,过点C作CE⊥AB于点E,
可得∠CBD=45°,∠CAD=60°,
设CE=x,
在Rt△CBE中,BE=CE=x,
在Rt△CAE中,AE=![]() x,
x,
∵AB=60(![]() +
+![]() )海里,
)海里,
∴x+![]() x=60(
x=60(![]() +
+![]() ),
),
解得:x=60![]() ,
,
则AC=![]() x=120
x=120![]() ,
,
BC=![]() x=120
x=120![]() ,
,
答:A与C的距离为120![]() 海里,B与C的距离为120
海里,B与C的距离为120![]() 里;
里;
(2)如图所示,过点D作DF⊥AC于点F,
在△ADF中,
∵AD=120(![]() -
-![]() ),∠CAD=60°,
),∠CAD=60°,
∴DF=ADsin60°=180![]() -60
-60![]() ≈106.8>100,
≈106.8>100,
故海监船沿AC前往C处盘查,无触礁的危险.

 考前必练系列答案
考前必练系列答案