题目内容
【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 . 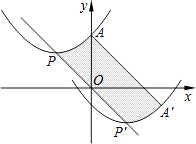
【答案】12
【解析】解:连接AP,A′P′,过点A作AD⊥PP′于点D, 由题意可得出:AP∥A′P′,AP=A′P′,
∴四边形APP′A′是平行四边形,
∵抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),
∴PO= ![]() =2
=2 ![]() ,∠AOP=45°,
,∠AOP=45°,
又∵AD⊥OP,
∴△ADO是等腰直角三角形,
∴PP′=2 ![]() ×2=4
×2=4 ![]() ,
,
∴AD=DO=sin45°OA= ![]() ×3=
×3= ![]() ,
,
∴抛物线上PA段扫过的区域(阴影部分)的面积为:4 ![]() ×
× ![]() =12.
=12.
故答案为:12.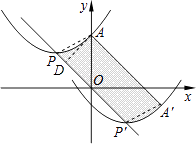
根据平移的性质得出四边形APP′A′是平行四边形,进而得出AD,PP′的长,求出面积即可.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
【题目】从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解”雾霾天气的主要原因“,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: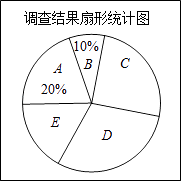
(1)填空:m= , n= . 扇形统计图中E组所占的百分比为%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?